



Next: Modal Logics
Up: Inference System
Previous: Restrictions for Inferences.
Contents
Sequent Calculus
Sequent calculus is usually viewed as being applied in a backward manner
to construct proofs for sequents 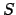 by eliminating the logical symbols in
by eliminating the logical symbols in 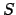 one after the other.
For this mode of application cuts are not required,
although their use might lead to much smaller proofs.
one after the other.
For this mode of application cuts are not required,
although their use might lead to much smaller proofs.
Saturation-based theorem proving can be viewed as a mechanism for
establishing
that is, for deriving the empty sequent 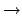 from an inconsistent
set
from an inconsistent
set
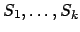 of sequents, by the forward application
of the rules of the sequent calculus.
In that context, the cut rule becomes the main working horse,
and its combination with the substitution rule,
which is an inverse form of certain quantifier rules,
is called resolution.
That view of resolution allows one to integrate
clausal normalform transformation into resolution and chaining
in a lazy manner.
of sequents, by the forward application
of the rules of the sequent calculus.
In that context, the cut rule becomes the main working horse,
and its combination with the substitution rule,
which is an inverse form of certain quantifier rules,
is called resolution.
That view of resolution allows one to integrate
clausal normalform transformation into resolution and chaining
in a lazy manner.
The (multi-conclusion) rules that we apply in a forward manner
are the inverse forms
of invertible rules such as
for the logical connectives.
(The expanded formula 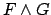 of the inference is called its main formula
below.)
The quantifier rules that we use are
of the inference is called its main formula
below.)
The quantifier rules that we use are
where 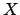 is a fresh free variable, and
is a fresh free variable, and
where 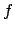 is a new (Skolem) function symbol and
is a new (Skolem) function symbol and 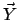 are the free variables
in
are the free variables
in 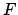 . (The ``left`` versions of the rules are analoguous.)
. (The ``left`` versions of the rules are analoguous.)
Note that these rules are simplifications in that the premise can be deleted
once its conclusions have been derived.
In fact, the conclusions imply their premise and are smaller in an appropriate extension
of the atom ordering to general first-order formulas.
However, we apply rules only if the main formula is either maximal in the sequent
or negative and selected. In other words, the rules obey the same restrictions with
respect to ordering and selection functions as the chaining inferences.
Sequents in Saturate may contain equalities
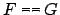 between formulas
between formulas
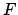 and
and 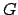 , semantically denoting equivalence of
, semantically denoting equivalence of 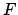 and
and 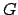 ,
which are dealt with specifically.
Only if a maximal one of the two sides
,
which are dealt with specifically.
Only if a maximal one of the two sides 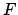 and
and 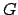 is non-atomic,
the equality is expanded according to
is non-atomic,
the equality is expanded according to
In case 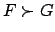 and
and 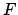 is atomic, i.e., of the form
is atomic, i.e., of the form
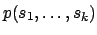 ,
with a predicate symbol
,
with a predicate symbol 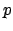 and terms
and terms 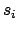 ,
the equivalence is not eliminated from the sequent.
Non-eliminated equivalences are subject to ordering-restricted forms of chaining
inferences such as
,
the equivalence is not eliminated from the sequent.
Non-eliminated equivalences are subject to ordering-restricted forms of chaining
inferences such as
with 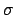 the mgu of the atoms
the mgu of the atoms 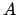 and
and 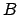 , provided
, provided
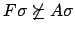 ,
,
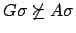 ,
no premise contains a selected literal, and both equivalences are maximal
in their respective premises.
,
no premise contains a selected literal, and both equivalences are maximal
in their respective premises.
Orientable equivalences
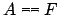 in which the maximal side
in which the maximal side 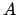 is atomic
are also used for simplification in that everywhere occurences of
is atomic
are also used for simplification in that everywhere occurences of 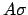 will be replaced
by
will be replaced
by 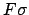 .
This handling of equivalences is especially useful for definition hierarchies
if the definitions are to be applied in a goal to replace derived predicates
and if one does not want to automatically
infer
lemmas for the new predicates.
An example how proofs in Saturate look like when
simplification with equivalences are intertwined with chaining
is a simple set theory
with
an ordering
under which definitions are expanded out.
.
This handling of equivalences is especially useful for definition hierarchies
if the definitions are to be applied in a goal to replace derived predicates
and if one does not want to automatically
infer
lemmas for the new predicates.
An example how proofs in Saturate look like when
simplification with equivalences are intertwined with chaining
is a simple set theory
with
an ordering
under which definitions are expanded out.




Next: Modal Logics
Up: Inference System
Previous: Restrictions for Inferences.
Contents
Harald Ganzinger
2002-12-04
Imprint | Data Protection
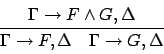
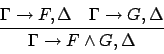
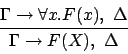
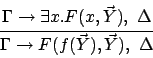
![]() between formulas
between formulas
![]() and
and ![]() , semantically denoting equivalence of
, semantically denoting equivalence of ![]() and
and ![]() ,
which are dealt with specifically.
Only if a maximal one of the two sides
,
which are dealt with specifically.
Only if a maximal one of the two sides ![]() and
and ![]() is non-atomic,
the equality is expanded according to
is non-atomic,
the equality is expanded according to
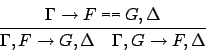
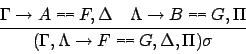
![]() in which the maximal side
in which the maximal side ![]() is atomic
are also used for simplification in that everywhere occurences of
is atomic
are also used for simplification in that everywhere occurences of ![]() will be replaced
by
will be replaced
by ![]() .
This handling of equivalences is especially useful for definition hierarchies
if the definitions are to be applied in a goal to replace derived predicates
and if one does not want to automatically
infer
lemmas for the new predicates.
An example how proofs in Saturate look like when
simplification with equivalences are intertwined with chaining
is a simple set theory
with
an ordering
under which definitions are expanded out.
.
This handling of equivalences is especially useful for definition hierarchies
if the definitions are to be applied in a goal to replace derived predicates
and if one does not want to automatically
infer
lemmas for the new predicates.
An example how proofs in Saturate look like when
simplification with equivalences are intertwined with chaining
is a simple set theory
with
an ordering
under which definitions are expanded out.