Universität des Saarlandes
Fachbereich 14 - Informatik

Dr. S. Schirra, Dr. E. Schömer
SOFTWAREPRAKTIKUM WS 99/00

1. Übungsblatt
(Abgabe: 25. - 29. Oktober 1999)


1.
Aufgabe:      EIN EINFACHES PROGRAMM (Punkte: 1)

Schreiben Sie ein kleines Programm, das zwei Zahlen einliest und Summe und Mittelwert der beiden Zahlen ausdruckt.

2.
Aufgabe:      FEHLERSUCHE (Punkte: 2)

Korrigieren Sie den Code in gcd_main.C, gcd.h und gcd.C. Benuzten Sie ein makefile und gegebenenfalls einen Debugger.

3.
Aufgabe:      ZWEI EINFACHE KLASSEN (Punkte: 7)

Entwerfen und Implementieren Sie eine Klasse Line für Geraden. Ein Objekt der Klasse Line soll aus zwei Objekten vom dem aus der Vorlesung bekannten Typ Point konstruiert werden können. Ebenso soll eine Line aus einem Punkt und zwei float Werten konstruiert werden können. Ferner soll es eine Memberfunktion float Line::distance(const Point&) geben, die den Abstand eines Punktes zu einer Geraden berechnet.

Hinweis:

Der Abstand d eines Punktes $\mathbf{c}=[c_1,c_2]^T\in\mathbf{R}^2$ von einer Gerade durch die Punkte $\mathbf{a}=[a_1,a_2]^T\in\mathbf{R}^2$ und $\mathbf{b}=[b_1,b_2]^T\in\mathbf{R}^2$ ist gegeben durch:

\begin{displaymath}d = \frac{\vert\mathbf{a}\times\mathbf{b}+\mathbf{c}\times (\... ...vert}{\sqrt{(\mathbf{b}-\mathbf{a})^T(\mathbf{b}-\mathbf{a})}} \end{displaymath}

Dabei sind das Skalarprodukt und das Kreuzprodukt für zwei Vektoren $\mathbf{u}=[u_1,u_2]^T,\mathbf{v}=[v_1,v_2]^T\in\mathbf{R}^2$ wie folgt definiert:

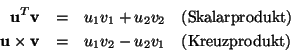
\begin{eqnarray*}\mathbf{u}^T\mathbf{v} &=& u_1 v_1 + u_2 v_2 \quad\mbox{(Skalar... ...\times\mathbf{v} &=& u_1 v_2 - u_2 v_1\quad\mbox{(Kreuzprodukt)} \end{eqnarray*}


Erweitern Sie die Klasse Point um Memberfunktionen float Point::distance(const Point&) und float Point::distance(const Line&), die den Abstand eines Punktes zu einem anderen Punkt bzw. einer Geraden berechnen.

4.
Aufgabe:      MANDELBROT UND JULIA MENGEN (Punkte: 10)

Wir wollen die fraktale Struktur der Mandelbrot und der Julia Mengen als Graustufen Bilder visualisieren, indem wir das Divergenzverhalten der iterierten Abbildung zi+1 = zi2+c in der komplexen Zahlenebene untersuchen.

Zur Berechnung der Mandelbrot Menge setzen wir z0=0 und bestimmen für jedes c aus dem Definitionsbereich die Zahl k(c) der Iterationen, so dass zk(c) erstmals außerhalb des Kreises um den Ursprung mit Radius 2 liegt:

\begin{displaymath}k(c) = \min\{i\geq 0\,\vert\,\vert z_i\vert>2\} \end{displaymath}

Die Helligkeit $f(c)\in[0..255]$ für einen Punkt c kann man z.B. wie folgt definieren:

\begin{displaymath}f(c)=\lfloor 2.55*(100-\min\{k(c),100\})\rfloor \end{displaymath}

Für $\Re(c)\in [-1.5,0.5]$ und $\Im(c)\in [-1.0,1.0]$ erhält man folgendes Ergebnis:
\epsffile{mandel.eps}
Zur Berechnung von Julia Mengen legt man c fest und lässt z0über einen gewissen Bereich variieren. Die Funktionen k und fhängen nun nicht mehr von c ab, sondern von z0. Einige interessante Ergebnisse erhält man für $\Re(z_0),\Im(z_0) \in[-1,1]$ und c=(-0.74543,0.11301), c=(-0.194,0.6557), c=(0.27334,0.00742) oder c=(0.11031,-0.67037).

Benutzen Sie die Klasse double_complex aus <complex> zur Realisierung der Arithmetik über den komplexen Zahlen und orientieren Sie sich zur Visualisierung an dem Beispielprogramm grey.C.