Universität des Saarlandes
Fachbereich 14 - Informatik

Dr. S. Schirra, Dr. E. Schömer

SOFTWAREPRAKTIKUM

3. Übungsblatt
(Abgabe: 8. - 12. November 1999)

1.

Aufgabe: SEGMENT KLASSE (Punkte: 2)

Implementieren Sie eine Klasse Segment für Strecken. Eine Strecke soll aus zwei Punkten konstruiert werden können. Implementieren Sie einen Copy-Konstruktor und eine Copy-Assignment Funktion (überlegen Sie sich, ob das für Ihre Segment Klasse nötig war).

2.

Aufgabe: OPERATOR OVERLOADING (Punkte: 4)

Erweitern Sie die Klasse Integral_double, so dass das Programm Integral_double_uebung.C compiliert und ohne assertion violation ausgeführt werden kann.

3.

Aufgabe: POINTERS TO FUNTION (Punkte: 4)

Die folgenden Funktionen sind in <cmath> definiert:

  double abs(double);
  double sin(double);
  double cos(double);
  double sqrt(double);

Schreiben Sie ein Programm, das ein Feld (array) von Zeigern (pointers) auf solche Funktionen definiert. Initialisieren Sie das Feld mit obigen Funktionen. Rufen Sie jede der Funktionen mindestens einmal mithilfe des Feldes mit einem (legalen) double-Argument Ihrer Wahl auf.

Hinweis: -lm beim Linken hinzufügen

4.

Aufgabe: SKALIERUNG VON RASTERDATEN (Punkte: 10)

Gegeben sei ein Graustufen-Rasterbild der Breite und der Höhe, das so skaliert werden soll, dass ein Bild der Breite und der Höhe entsteht. Die Rasterbilder wollen wir als zwei Abbildungen und auffassen.

	$\displaystyle F,G:\;\mathbf{Z}\times\mathbf{Z}\rightarrow\mathbf{R}$
	$\displaystyle (i,j)\mapsto F(i,j)$ für $\displaystyle \quad i\in [0..w_F-1]\;$ und $\displaystyle \; j\in [0..h_F-1]$
	$\displaystyle (i,j)\mapsto G(i,j)$ für $\displaystyle \quad i\in [0..w_G-1]\;$ und $\displaystyle \; j\in [0..h_G-1]$

Wir setzen wie folgt fort:

	$\displaystyle f:\;\mathbf{R}\times\mathbf{R}\rightarrow\mathbf{R}$
	$\displaystyle f(x,y) = F(\lfloor x\rfloor,\lfloor y\rfloor)$ für $\displaystyle \quad x\in [0,w_F-1]\;$ und $\displaystyle \;y\in [0,h_F-1]$
	wobei $\displaystyle \quad \lfloor x \rfloor =$ größte ganze Zahl $\displaystyle \leq x$

Die Abbildung können wir wie folgt definieren:

	$\displaystyle G(i,j) = \int_{i w}^{(i+1)w}\int_{j h}^{(j+1)h} f(x,y) dx dy$ für $\displaystyle \quad i\in [0..w_G-1]\;$ und $\displaystyle \; j\in [0..h_G-1]$
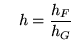	wobei $\displaystyle \quad w=\frac{w_F}{w_G}$ und $\displaystyle \quad h=\frac{h_F}{h_G}$

Ein Beispiel:

$\epsffile {scale10.eps}$

$\Longrightarrow$

$\epsffile {scale7.eps}$

Entwerfen Sie eine Klasse für die Repräsentation von Graustufen-Rasterbildern und realisieren Sie die Skalierungsoperation nach obigem Vorbild. Visualisieren Sie die Ergebnisse mit Hilfe der OpenGL-Funktion glDrawPixels ...