Specific Treatment of Binary Relations

Saturate attempts to automatically recognize certain properties of binary relations and then specializes the chaining-based inference rules accordingly. Also, the simplification module will know about these properties. The system recognizes and treats in a specific manner

transitivity

or, more generally, certain collections of composition laws of the form

$$p(X,Y), q(Y,Z) \to r(X,Z),$$

for binary relations 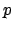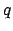$p$, $q$, and $r$;

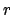totality laws

of the form

$$\to p(X,Y), p(Y,X), X=Y ;$$

reflexivity and irreflexivity laws

of the form

$$\to p(X,X)$$

or

$$p(X,X) \to ;$$

monotonicity laws

of the form

$$p(X,Y) \to p(f(\ldots X \ldots),f(\ldots Y \ldots)) ;$$

anti-monotonicity laws

of the form

$$p(X,Y) \to p(f(\ldots Y \ldots),f(\ldots X \ldots)) ;$$

symmetry laws

of the form

$$\to p(X,Y) , p(Y,X) ;$$

density laws

of the form

$$p(X,Y) \to p(X,d(X,Y)) \wedge p(d(X,Y),Y)$$

(written as two clauses); and

laws about the absense of endpoints

of the form

$$\to p(X,f(X))$$

or

$$\to p(g(X),X).$$

Interesting types of binary relations with such properties include equivalences, equality (congruences) and orderings.

Imprint | Data Protection