



Next: Context-free Syntax for Clauses.
Up: The Saturate System
Previous: Getting started
Contents
Formula Syntax
First-order formulas
are built in from
- Prolog variables, denoting free or bound variables,
- logical symbols =,
~, and, or, <=>, =>,
all, and exists, denoting equality, negation, conjunction, disjunction,
equivalence, implication, universal and existential quantification, respectively, and
- Prolog terms for denoting terms and atoms.
General or standard first-order clauses are written as
sequents
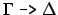 of multisets
of multisets 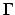 (the antecedent)
and
(the antecedent)
and 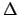 (the succedent)
of general literals.
The elements in
(the succedent)
of general literals.
The elements in 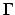 and
and 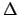 are separated by ``,''.
A general literal
is either a first-order formulas
are separated by ``,''.
A general literal
is either a first-order formulas 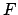 or, somewhat unusually,
an equality
or, somewhat unusually,
an equality
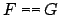 between two
formulas
between two
formulas 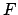 and
and 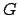 .
As usual, comma on the right side of
.
As usual, comma on the right side of
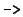 denotes disjunction, and comma left denotes
conjunction. Equality on the level of formulas denotes logical equivalence.
This is an example of a sequent consisting of a single (and positive)
equality:
denotes disjunction, and comma left denotes
conjunction. Equality on the level of formulas denotes logical equivalence.
This is an example of a sequent consisting of a single (and positive)
equality:
-> eq(X,Y) == all(Z,member(Z,X) <=> member(Z,Y))
Free variables in a clause, such as 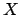 and
and 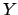 above,
are implicitly universally quantified.
Here is an example of a (Horn) sequent
above,
are implicitly universally quantified.
Here is an example of a (Horn) sequent
exists(X,f(X)), exists(X,g(X)) ->
all(X,(f(X) => h(X)) and all(X,g(X)=>j(X)))
==
all(X,all(Y,f(X) and g(Y) => h(X) and j(Y)))
with a 2-element antecedent and an
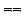 -equality
as succedent.
We have an equivalence == on the level of sequents
(in addition to the equivalence <=> on the level of formulas)
as an explicit
indication for our computing with certain such equivalences
by rewriting.
A detailed definition of the syntax is given below.
-equality
as succedent.
We have an equivalence == on the level of sequents
(in addition to the equivalence <=> on the level of formulas)
as an explicit
indication for our computing with certain such equivalences
by rewriting.
A detailed definition of the syntax is given below.
Subsections




Next: Context-free Syntax for Clauses.
Up: The Saturate System
Previous: Getting started
Contents
Harald Ganzinger
2002-12-04
Imprint | Data Protection