Ordering Declarations

$next$ $up$ $previous$ $contents$
Next: Precedence Declarations Up: add: Adding Input Previous: Predicate Declarations Contents

By an optional declaration of the form

$\begin{displaymath} \mbox{{\tt ordering($Ord$)}}. \end{displaymath}$

one specifies the (kind of the) termination ordering to be used for ordered inferences and for redundancy proofs.

may be either

lpo, for the lexicographic path ordering which is the default setting, or
aclpo for the AC-lexicographic path ordering which is the default setting when AC-operators are present,
sto for a precedence-based subterm ordering, or
poly for (linear) polynomial interpretations²

The sto ordering is the union of the subterm ordering with inequations 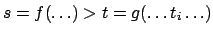$s=f(\ldots) > t=g(\ldots t_i \ldots)$ such that any of the

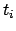are subterms of

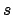and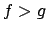

in the precedence. The atom ordering is a certain lexicographic extension of this term ordering.

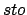is useful, probably, only in the non-equational case when one tries to prove locality of an inference system, cf. ocality and saturation.

Harald Ganzinger 2002-12-04