



Next: Examples
Up: add: Adding Input
Previous: Calls to Flag Settings
Contents
Options Settings
Option settings are of the form
where
O : term_size_weight | term_var_weight | term_var_weight_gt_small |
normal_term_weight | increment(N) | var_depth(N) |
special_relations(on) | special_relations(off) |
ac(on) | ac(off) |
memo_constraints(on) | memo_constraints(off)
The weight options set the weight function for terms and clauses
which is used for inference selection.
- term_ size_ weight
- :
weight = number of nodes in a term
- term_ var_ weight
weight = weighted product of term size, term depth
and number of different variables
- term_ var_ weight_ gt_ small
- similar, except that ground terms
are made very small
- normal_ term_ weight
- (default)
weight = weighted product of term size
and depth
- increment(
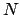 )
)
- Inferences are computed from clauses up to a certain
weight. If no proof is found, the bound is increased by
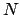 . Defaults:
. Defaults:
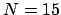 for term_ size_ weight, normal_ term_ weight,
for term_ size_ weight, normal_ term_ weight,
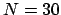 , otherwise.
, otherwise.
- var_ depth(N)
- Clauses are preprocessed into rules in an order that also
depends on the number of different variables occuring in it.
If this number exceeds
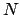 (default value is 3), processing of the clause
is delayed.
(default value is 3), processing of the clause
is delayed.
- special_ relations(
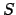 )
)
-
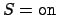 turns on the special treatment of
transitive relations by chaining inferences; default.
In this mode, transitivity, reflexivity, irreflexivity
totality, density and no endpoint axioms are treated
specifically. Saturate recognizes these properties
automatically, provided they are not hidden, i.e.,
follow in a non-trivial way from other properties.
Actually Saturate should be more clever in recognizing
these properties.
turns on the special treatment of
transitive relations by chaining inferences; default.
In this mode, transitivity, reflexivity, irreflexivity
totality, density and no endpoint axioms are treated
specifically. Saturate recognizes these properties
automatically, provided they are not hidden, i.e.,
follow in a non-trivial way from other properties.
Actually Saturate should be more clever in recognizing
these properties.
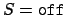 : transitive relations are treated as any other
predicate.
This option should be specified textually before
any axioms for the respective predicates.
This option essentially reduces the inference system
to ordered resolution. It should be used when Saturate is
applied in order to prove the <locality
of a Horn theory.
: transitive relations are treated as any other
predicate.
This option should be specified textually before
any axioms for the respective predicates.
This option essentially reduces the inference system
to ordered resolution. It should be used when Saturate is
applied in order to prove the <locality
of a Horn theory.
- ac(S)
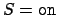 (default) results in employing AC-superposition
based on AC-unification and extended rules for AC symbols.
(default) results in employing AC-superposition
based on AC-unification and extended rules for AC symbols.
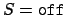 results in the treatment of AC-symbols by ordered rewriting.This option
must textually preceed any AC laws.
results in the treatment of AC-symbols by ordered rewriting.This option
must textually preceed any AC laws.
- memo_ constraints(S)
-
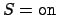 switches memoization for ordering constraints on.
This is the recommended setting for cases in which big
ordering constraints are generated. This is the case in
particular when clausal rewriting is turned on.
switches memoization for ordering constraints on.
This is the recommended setting for cases in which big
ordering constraints are generated. This is the case in
particular when clausal rewriting is turned on.
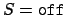 (default): no memoization
(default): no memoization
option/1 may also be called interactively.




Next: Examples
Up: add: Adding Input
Previous: Calls to Flag Settings
Contents
Harald Ganzinger
2002-12-04
Imprint | Data Protection
![]() : transitive relations are treated as any other
predicate.
This option should be specified textually before
any axioms for the respective predicates.
This option essentially reduces the inference system
to ordered resolution. It should be used when Saturate is
applied in order to prove the <locality
of a Horn theory.
: transitive relations are treated as any other
predicate.
This option should be specified textually before
any axioms for the respective predicates.
This option essentially reduces the inference system
to ordered resolution. It should be used when Saturate is
applied in order to prove the <locality
of a Horn theory.
![]() results in the treatment of AC-symbols by ordered rewriting.This option
must textually preceed any AC laws.
results in the treatment of AC-symbols by ordered rewriting.This option
must textually preceed any AC laws.
![]() (default): no memoization
(default): no memoization