



Next: Saturation of a Theory
Up: Applications
Previous: Applications
Contents
Refutational Theorem Proving
In refutational theorem proving we prove 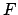 by deriving a contradiction
from
by deriving a contradiction
from 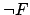 .
For simple cases, calling prove
will do the job.
The formula
.
For simple cases, calling prove
will do the job.
The formula
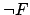 will be saturated up to redundancy by
a refutationally complete inference system
until a contradiction is found.
Alternatively, if
will be saturated up to redundancy by
a refutationally complete inference system
until a contradiction is found.
Alternatively, if 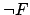 can be finitely saturated
without producing a contradiction,
can be finitely saturated
without producing a contradiction, 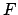 is not provable.
Applying simplification and techniques for detecting redundancy,
Saturate attempts to gain better control of its forward computation
mode.
The forward inferences (resolution, chaining, superposition)
are restricted by ordering constraints and selection functions
such that only maximal or selected atoms or terms need
to be resolved or chained.
is not provable.
Applying simplification and techniques for detecting redundancy,
Saturate attempts to gain better control of its forward computation
mode.
The forward inferences (resolution, chaining, superposition)
are restricted by ordering constraints and selection functions
such that only maximal or selected atoms or terms need
to be resolved or chained.
When one uses Saturate for refutational theorem proving,
only a modest amount of simplification should
be applied. If Saturate is at all able to find a proof,
if will often also find a proof in its automatic mode which
in particular includes an automatic setting of the ordering and selection
function. Sometimes a more clever setting of meta-logical directives
is required. A more detailed discussion of this issue is
provided below.




Next: Saturation of a Theory
Up: Applications
Previous: Applications
Contents
Harald Ganzinger
2002-12-04
Imprint | Data Protection