
[ 1st Edition ] [ Free Newsletter ]
[ Seminars ] [ Seminars on CD ROM ] [ Consulting ]

It’s a fairly simple program
that has only a fixed quantity of objects with known lifetimes.
In general, your programs will always be
creating new objects based on some criteria that will be known only at the time
the program is running. You won’t know until run-time the quantity or even
the exact type of the objects you need. To solve the general programming
problem, you need to be able to create any number of objects, anytime, anywhere.
So you can’t rely on creating a named reference to hold each one of your
objects:
MyObject myReference;
since you’ll never know how many of
these you’ll actually need.
To solve this rather essential problem,
Java has several ways to hold objects (or rather, references to objects). The
built-in type is the array, which has been discussed before. Also, the Java
utilities library has a reasonably complete set of
container classes (also known as
collection classes, but because the Java 2
libraries use the name Collection to refer to a particular subset of the
library, I shall use the more inclusive term “container”).
Containers provide sophisticated ways to hold and even manipulate your
objects.
Most of the necessary introduction to
arrays is in the last section of Chapter 4, which showed
how you define and initialize an array. Holding objects is the focus of this
chapter, and an array is just one way to hold objects. But there are a number of
other ways to hold objects, so what makes an array special?
There are two issues that distinguish
arrays from other types of containers: efficiency and
type. The array is the most efficient way that Java
provides to store and randomly access a sequence of objects (actually, object
references). The array is a simple linear sequence, which makes element access
fast, but you pay for this speed: when you create an array object, its size is
fixed and cannot be changed for the lifetime of that array object. You might
suggest creating an array of a particular size and then, if you run out of
space, creating a new one and moving all the references from the old one to the
new one. This is the behavior of the ArrayList class, which will be
studied later in this chapter. However, because of the overhead of this size
flexibility, an ArrayList is measurably less efficient than an
array.
The vector
container class in C++ does know the type of objects it holds, but it has
a different drawback when compared with arrays in Java: the C++
vector’s operator[] doesn’t do bounds checking, so you
can run past the
end[45]. In Java,
you get bounds checking regardless of whether you’re using an array or a
container—you’ll get a
RuntimeException if you exceed the bounds. As
you’ll learn in Chapter 10, this type of exception indicates a programmer
error, and thus you don’t need to check for it in your code. As an aside,
the reason the C++ vector doesn’t check bounds with every access is
speed—in Java you have the constant performance overhead of bounds
checking all the time for both arrays and containers.
The other generic container classes that
will be studied in this chapter, List,
Set, and Map, all
deal with objects as if they had no specific type. That is, they treat them as
type Object, the root class of all classes in
Java. This works fine from one standpoint: you need to build only one container,
and any Java object will go into that container. (Except for
primitives—these can be placed in containers as constants using the Java
primitive wrapper classes, or as changeable values by wrapping in your own
class.) This is the second place where an array is superior to the generic
containers: when you create an array, you create it to hold a specific type.
This means that you get compile-time type checking to prevent you from putting
the wrong type in, or mistaking the type that you’re extracting. Of
course, Java will prevent you from sending an inappropriate message to an
object, either at compile-time or at run-time. So it’s not much riskier
one way or the other, it’s just nicer if the compiler points it out to
you, faster at run-time, and there’s less likelihood that the end user
will get surprised by an exception.
For efficiency and type checking
it’s always worth trying to use an array if you can. However, when
you’re trying to solve a more general problem arrays can be too
restrictive. After looking at arrays, the rest of this chapter will be devoted
to the container classes provided by
Java.
Regardless of what type of array
you’re working with, the array identifier is actually a reference to a
true object that’s created on the heap. This is the object that holds the
references to the other objects, and it can be created either implicitly, as
part of the array initialization syntax, or explicitly with a new
expression. Part of the array object (in fact, the only field or method you can
access) is the read-only length member that tells you how many elements
can be stored in that array object.
The ‘[]’ syntax
is the only other access that you have to the array object.
The following example shows the various
ways that an array can be initialized, and how the array references can be
assigned to different array objects. It also shows that
arrays of objects and arrays of
primitives are almost identical in their use. The only difference is that arrays
of objects hold references, while arrays of primitives hold the primitive values
directly.
//: c09:ArraySize.java
// Initialization & re-assignment of arrays.
class Weeble {} // A small mythical creature
public class ArraySize {
public static void main(String[] args) {
// Arrays of objects:
Weeble[] a; // Null reference
Weeble[] b = new Weeble[5]; // Null references
Weeble[] c = new Weeble[4];
for(int i = 0; i < c.length; i++)
c[i] = new Weeble();
// Aggregate initialization:
Weeble[] d = {
new Weeble(), new Weeble(), new Weeble()
};
// Dynamic aggregate initialization:
a = new Weeble[] {
new Weeble(), new Weeble()
};
// Compile error: variable a not initialized:
//!System.out.println("a.length=" + a.length);
System.out.println("b.length = " + b.length);
// The references inside the array are
// automatically initialized to null:
for(int i = 0; i < b.length; i++)
System.out.println("b[" + i + "]=" + b[i]);
System.out.println("c.length = " + c.length);
System.out.println("d.length = " + d.length);
a = d;
System.out.println("a.length = " + a.length);
System.out.println("a.length = " + a.length);
// Arrays of primitives:
int[] e; // Null reference
int[] f = new int[5];
int[] g = new int[4];
for(int i = 0; i < g.length; i++)
g[i] = i*i;
int[] h = { 11, 47, 93 };
// Compile error: variable e not initialized:
//!System.out.println("e.length=" + e.length);
System.out.println("f.length = " + f.length);
// The primitives inside the array are
// automatically initialized to zero:
for(int i = 0; i < f.length; i++)
System.out.println("f[" + i + "]=" + f[i]);
System.out.println("g.length = " + g.length);
System.out.println("h.length = " + h.length);
e = h;
System.out.println("e.length = " + e.length);
e = new int[] { 1, 2 };
System.out.println("e.length = " + e.length);
}
} ///:~Here’s the output from the
program:
b.length = 5 b[0]=null b[1]=null b[2]=null b[3]=null b[4]=null c.length = 4 d.length = 3 a.length = 3 a.length = 2 f.length = 5 f[0]=0 f[1]=0 f[2]=0 f[3]=0 f[4]=0 g.length = 4 h.length = 3 e.length = 3 e.length = 2
The array a is initially just a
null reference, and the compiler prevents you from
doing anything with this reference until you’ve properly initialized it.
The array b is initialized to point to an array of Weeble
references, but no actual Weeble objects are ever placed in that array.
However, you can still ask what the size of the array is, since b is
pointing to a legitimate object. This brings up a slight drawback: you
can’t find out how many elements are actually in the array, since
length tells you only how many elements can be placed in the
array; that is, the size of the array object, not the number of elements it
actually holds. However, when an array object is created its references are
automatically initialized to null, so you can see whether a particular
array slot has an object in it by checking to see whether it’s
null. Similarly, an array of primitives is automatically initialized to
zero for numeric types, (char)0 for char, and false for
boolean.
Array c shows the creation of the
array object followed by the assignment of Weeble objects to all the
slots in the array. Array d shows the “aggregate
initialization” syntax that causes the array object to be created
(implicitly with new on the heap, just like for array c)
and initialized with Weeble objects, all in one
statement.
The
next array initialization could be thought of as a “dynamic aggregate
initialization.” The aggregate initialization used by d must be
used at the point of d’s definition, but with the second syntax you
can create and initialize an array object anywhere. For example, suppose
hide( ) is a method that takes an array of Weeble objects.
You could call it by saying:
hide(d);
but you can also dynamically create the
array you want to pass as the argument:
hide(new Weeble[] { new Weeble(), new Weeble() });In some situations this new syntax
provides a more convenient way to write code.
The expression
a = d;
shows how you can take a reference
that’s attached to one array object and assign it to another array object,
just as you can do with any other type of object reference. Now both a
and d are pointing to the same array object on the heap.
The second part of ArraySize.java
shows that primitive arrays work just like object arrays except that
primitive arrays hold the primitive values
directly.
Container classes can hold only
references to objects. An array, however, can be created to hold primitives
directly, as well as references to objects. It is possible to use the
“wrapper” classes such as Integer, Double, etc. to
place primitive values inside a container, but the wrapper classes for
primitives can be awkward to use. In addition, it’s much more efficient to
create and access an array of primitives than a container of wrapped
primitives.
Of course, if you’re using a
primitive type and you need the flexibility of a container that automatically
expands when more space is needed, the array won’t work and you’re
forced to use a container of wrapped primitives. You might think that there
should be a specialized type of ArrayList for each of the primitive data
types, but Java doesn’t provide this for you. Some sort of templatizing
mechanism might someday provide a better way for Java to handle this
problem.[46]
Suppose you’re writing a method and
you don’t just want to return just one thing, but a whole bunch of things.
Languages like C and C++ make this difficult because you can’t just return
an array, only a pointer to an array. This introduces problems because it
becomes messy to control the lifetime of the array, which easily leads to memory
leaks.
Java
takes a similar approach, but you just “return an array.” Actually,
of course, you’re returning a reference to an array, but with Java you
never worry about responsibility for that array—it will be around as long
as you need it, and the garbage collector will clean it up when you’re
done.
As an example, consider returning an
array of String:
//: c09:IceCream.java
// Returning arrays from methods.
public class IceCream {
static String[] flav = {
"Chocolate", "Strawberry",
"Vanilla Fudge Swirl", "Mint Chip",
"Mocha Almond Fudge", "Rum Raisin",
"Praline Cream", "Mud Pie"
};
static String[] flavorSet(int n) {
// Force it to be positive & within bounds:
n = Math.abs(n) % (flav.length + 1);
String[] results = new String[n];
boolean[] picked =
new boolean[flav.length];
for (int i = 0; i < n; i++) {
int t;
do
t = (int)(Math.random() * flav.length);
while (picked[t]);
results[i] = flav[t];
picked[t] = true;
}
return results;
}
public static void main(String[] args) {
for(int i = 0; i < 20; i++) {
System.out.println(
"flavorSet(" + i + ") = ");
String[] fl = flavorSet(flav.length);
for(int j = 0; j < fl.length; j++)
System.out.println("\t" + fl[j]);
}
}
} ///:~The method flavorSet( )
creates an array of String called results. The size of this array
is n, determined by the argument you pass into the method. Then it
proceeds to choose flavors randomly from the array flav and place them
into results, which it finally returns. Returning an array is just like
returning any other object—it’s a reference. It’s not
important that the array was created within flavorSet( ), or that
the array was created anyplace else, for that matter. The garbage collector
takes care of cleaning up the array when you’re done with it, and the
array will persist for as long as you need it.
As an aside, notice that when
flavorSet( ) chooses flavors randomly, it ensures that a random
choice hasn’t been picked before. This is performed in a do loop
that keeps making random choices until it finds one that’s not already in
the picked array. (Of course, a String comparison could also have
been performed to see if the random choice was already in the results
array, but String comparisons are inefficient.) If it’s successful,
it adds the entry and finds the next one (i gets incremented).
main( ) prints out 20 full
sets of flavors, so you can see that flavorSet( ) chooses the
flavors in a random order each time. It’s easiest to see this if you
redirect the output into a file. And while you’re looking at the file,
remember, you just want the ice cream, you don’t need
it.
In java.util, you’ll find
the Arrays class, which holds a set of
static methods that perform utility functions for arrays. There are four
basic functions: equals( ), to compare two arrays for equality;
fill( ), to fill an array with a value; sort( ), to sort
the array; and binarySearch( ), to find an element in a sorted
array. All of these methods are overloaded for all the primitive types and
Objects. In addition, there’s a single asList( ) method
that takes any array and turns it into a List container—which
you’ll learn about later in this chapter.
While useful, the Arrays class
stops short of being fully functional. For example, it would be nice to be able
to easily print the elements of an array without having to code a for
loop by hand every time. And as you’ll see, the fill( ) method
only takes a single value and places it in the array, so if you wanted—for
example—to fill an array with randomly generated numbers,
fill( ) is no help.
Thus it makes sense to supplement the
Arrays class with some additional utilities, which will be placed in the
package com.bruceeckel.util for convenience. These will print an
array of any type, and fill an array with values or objects that are created by
an object called a generator that you can define.
Because code needs
to be created for each primitive type as well as Object, there’s a
lot of nearly duplicated
code[47]. For
example, a “generator” interface is required for each type because
the return type of next( ) must be different in each
case:
//: com:bruceeckel:util:Generator.java
package com.bruceeckel.util;
public interface Generator {
Object next();
} ///:~
//: com:bruceeckel:util:BooleanGenerator.java
package com.bruceeckel.util;
public interface BooleanGenerator {
boolean next();
} ///:~
//: com:bruceeckel:util:ByteGenerator.java
package com.bruceeckel.util;
public interface ByteGenerator {
byte next();
} ///:~
//: com:bruceeckel:util:CharGenerator.java
package com.bruceeckel.util;
public interface CharGenerator {
char next();
} ///:~
//: com:bruceeckel:util:ShortGenerator.java
package com.bruceeckel.util;
public interface ShortGenerator {
short next();
} ///:~
//: com:bruceeckel:util:IntGenerator.java
package com.bruceeckel.util;
public interface IntGenerator {
int next();
} ///:~
//: com:bruceeckel:util:LongGenerator.java
package com.bruceeckel.util;
public interface LongGenerator {
long next();
} ///:~
//: com:bruceeckel:util:FloatGenerator.java
package com.bruceeckel.util;
public interface FloatGenerator {
float next();
} ///:~
//: com:bruceeckel:util:DoubleGenerator.java
package com.bruceeckel.util;
public interface DoubleGenerator {
double next();
} ///:~Arrays2
contains a variety of print( ) functions, overloaded for each type.
You can simply print an array, you can add a message before the array is
printed, or you can print a range of elements within an array. The
print( ) code is self-explanatory:
//: com:bruceeckel:util:Arrays2.java
// A supplement to java.util.Arrays, to provide
// additional useful functionality when working
// with arrays. Allows any array to be printed,
// and to be filled via a user-defined
// "generator" object.
package com.bruceeckel.util;
import java.util.*;
public class Arrays2 {
private static void
start(int from, int to, int length) {
if(from != 0 || to != length)
System.out.print("["+ from +":"+ to +"] ");
System.out.print("(");
}
private static void end() {
System.out.println(")");
}
public static void print(Object[] a) {
print(a, 0, a.length);
}
public static void
print(String msg, Object[] a) {
System.out.print(msg + " ");
print(a, 0, a.length);
}
public static void
print(Object[] a, int from, int to){
start(from, to, a.length);
for(int i = from; i < to; i++) {
System.out.print(a[i]);
if(i < to -1)
System.out.print(", ");
}
end();
}
public static void print(boolean[] a) {
print(a, 0, a.length);
}
public static void
print(String msg, boolean[] a) {
System.out.print(msg + " ");
print(a, 0, a.length);
}
public static void
print(boolean[] a, int from, int to) {
start(from, to, a.length);
for(int i = from; i < to; i++) {
System.out.print(a[i]);
if(i < to -1)
System.out.print(", ");
}
end();
}
public static void print(byte[] a) {
print(a, 0, a.length);
}
public static void
print(String msg, byte[] a) {
System.out.print(msg + " ");
print(a, 0, a.length);
}
public static void
print(byte[] a, int from, int to) {
start(from, to, a.length);
for(int i = from; i < to; i++) {
System.out.print(a[i]);
if(i < to -1)
System.out.print(", ");
}
end();
}
public static void print(char[] a) {
print(a, 0, a.length);
}
public static void
print(String msg, char[] a) {
System.out.print(msg + " ");
print(a, 0, a.length);
}
public static void
print(char[] a, int from, int to) {
start(from, to, a.length);
for(int i = from; i < to; i++) {
System.out.print(a[i]);
if(i < to -1)
System.out.print(", ");
}
end();
}
public static void print(short[] a) {
print(a, 0, a.length);
}
public static void
print(String msg, short[] a) {
System.out.print(msg + " ");
print(a, 0, a.length);
}
public static void
print(short[] a, int from, int to) {
start(from, to, a.length);
for(int i = from; i < to; i++) {
System.out.print(a[i]);
if(i < to - 1)
System.out.print(", ");
}
end();
}
public static void print(int[] a) {
print(a, 0, a.length);
}
public static void
print(String msg, int[] a) {
System.out.print(msg + " ");
print(a, 0, a.length);
}
public static void
print(int[] a, int from, int to) {
start(from, to, a.length);
for(int i = from; i < to; i++) {
System.out.print(a[i]);
if(i < to - 1)
System.out.print(", ");
}
end();
}
public static void print(long[] a) {
print(a, 0, a.length);
}
public static void
print(String msg, long[] a) {
System.out.print(msg + " ");
print(a, 0, a.length);
}
public static void
print(long[] a, int from, int to) {
start(from, to, a.length);
for(int i = from; i < to; i++) {
System.out.print(a[i]);
if(i < to - 1)
System.out.print(", ");
}
end();
}
public static void print(float[] a) {
print(a, 0, a.length);
}
public static void
print(String msg, float[] a) {
System.out.print(msg + " ");
print(a, 0, a.length);
}
public static void
print(float[] a, int from, int to) {
start(from, to, a.length);
for(int i = from; i < to; i++) {
System.out.print(a[i]);
if(i < to - 1)
System.out.print(", ");
}
end();
}
public static void print(double[] a) {
print(a, 0, a.length);
}
public static void
print(String msg, double[] a) {
System.out.print(msg + " ");
print(a, 0, a.length);
}
public static void
print(double[] a, int from, int to){
start(from, to, a.length);
for(int i = from; i < to; i++) {
System.out.print(a[i]);
if(i < to - 1)
System.out.print(", ");
}
end();
}
// Fill an array using a generator:
public static void
fill(Object[] a, Generator gen) {
fill(a, 0, a.length, gen);
}
public static void
fill(Object[] a, int from, int to,
Generator gen){
for(int i = from; i < to; i++)
a[i] = gen.next();
}
public static void
fill(boolean[] a, BooleanGenerator gen) {
fill(a, 0, a.length, gen);
}
public static void
fill(boolean[] a, int from, int to,
BooleanGenerator gen) {
for(int i = from; i < to; i++)
a[i] = gen.next();
}
public static void
fill(byte[] a, ByteGenerator gen) {
fill(a, 0, a.length, gen);
}
public static void
fill(byte[] a, int from, int to,
ByteGenerator gen) {
for(int i = from; i < to; i++)
a[i] = gen.next();
}
public static void
fill(char[] a, CharGenerator gen) {
fill(a, 0, a.length, gen);
}
public static void
fill(char[] a, int from, int to,
CharGenerator gen) {
for(int i = from; i < to; i++)
a[i] = gen.next();
}
public static void
fill(short[] a, ShortGenerator gen) {
fill(a, 0, a.length, gen);
}
public static void
fill(short[] a, int from, int to,
ShortGenerator gen) {
for(int i = from; i < to; i++)
a[i] = gen.next();
}
public static void
fill(int[] a, IntGenerator gen) {
fill(a, 0, a.length, gen);
}
public static void
fill(int[] a, int from, int to,
IntGenerator gen) {
for(int i = from; i < to; i++)
a[i] = gen.next();
}
public static void
fill(long[] a, LongGenerator gen) {
fill(a, 0, a.length, gen);
}
public static void
fill(long[] a, int from, int to,
LongGenerator gen) {
for(int i = from; i < to; i++)
a[i] = gen.next();
}
public static void
fill(float[] a, FloatGenerator gen) {
fill(a, 0, a.length, gen);
}
public static void
fill(float[] a, int from, int to,
FloatGenerator gen) {
for(int i = from; i < to; i++)
a[i] = gen.next();
}
public static void
fill(double[] a, DoubleGenerator gen) {
fill(a, 0, a.length, gen);
}
public static void
fill(double[] a, int from, int to,
DoubleGenerator gen){
for(int i = from; i < to; i++)
a[i] = gen.next();
}
private static Random r = new Random();
public static class RandBooleanGenerator
implements BooleanGenerator {
public boolean next() {
return r.nextBoolean();
}
}
public static class RandByteGenerator
implements ByteGenerator {
public byte next() {
return (byte)r.nextInt();
}
}
static String ssource =
"ABCDEFGHIJKLMNOPQRSTUVWXYZ" +
"abcdefghijklmnopqrstuvwxyz";
static char[] src = ssource.toCharArray();
public static class RandCharGenerator
implements CharGenerator {
public char next() {
int pos = Math.abs(r.nextInt());
return src[pos % src.length];
}
}
public static class RandStringGenerator
implements Generator {
private int len;
private RandCharGenerator cg =
new RandCharGenerator();
public RandStringGenerator(int length) {
len = length;
}
public Object next() {
char[] buf = new char[len];
for(int i = 0; i < len; i++)
buf[i] = cg.next();
return new String(buf);
}
}
public static class RandShortGenerator
implements ShortGenerator {
public short next() {
return (short)r.nextInt();
}
}
public static class RandIntGenerator
implements IntGenerator {
private int mod = 10000;
public RandIntGenerator() {}
public RandIntGenerator(int modulo) {
mod = modulo;
}
public int next() {
return r.nextInt() % mod;
}
}
public static class RandLongGenerator
implements LongGenerator {
public long next() { return r.nextLong(); }
}
public static class RandFloatGenerator
implements FloatGenerator {
public float next() { return r.nextFloat(); }
}
public static class RandDoubleGenerator
implements DoubleGenerator {
public double next() {return r.nextDouble();}
}
} ///:~To fill an array of elements using a
generator, the fill( ) method takes a reference to an appropriate
generator interface, which has a next( ) method that will
somehow produce an object of the right type (depending on how the interface is
implemented). The fill( ) method simply calls next( )
until the desired range has been filled. Now you can create any generator by
implementing the appropriate interface, and use your generator with
fill( ).
Random data generators are useful for
testing, so a set of inner classes is created to implement all the primitive
generator interfaces, as well as a String generator to represent
Object. You can see that RandStringGenerator uses
RandCharGenerator to fill an array of characters, which is then turned
into a String. The size of the array is determined by the constructor
argument.
To generate numbers that aren’t too
large, RandIntGenerator defaults to a modulus of 10,000, but the
overloaded constructor allows you to choose a smaller value.
Here’s a program to test the
library, and to demonstrate how it is used:
//: c09:TestArrays2.java
// Test and demonstrate Arrays2 utilities
import com.bruceeckel.util.*;
public class TestArrays2 {
public static void main(String[] args) {
int size = 6;
// Or get the size from the command line:
if(args.length != 0)
size = Integer.parseInt(args[0]);
boolean[] a1 = new boolean[size];
byte[] a2 = new byte[size];
char[] a3 = new char[size];
short[] a4 = new short[size];
int[] a5 = new int[size];
long[] a6 = new long[size];
float[] a7 = new float[size];
double[] a8 = new double[size];
String[] a9 = new String[size];
Arrays2.fill(a1,
new Arrays2.RandBooleanGenerator());
Arrays2.print(a1);
Arrays2.print("a1 = ", a1);
Arrays2.print(a1, size/3, size/3 + size/3);
Arrays2.fill(a2,
new Arrays2.RandByteGenerator());
Arrays2.print(a2);
Arrays2.print("a2 = ", a2);
Arrays2.print(a2, size/3, size/3 + size/3);
Arrays2.fill(a3,
new Arrays2.RandCharGenerator());
Arrays2.print(a3);
Arrays2.print("a3 = ", a3);
Arrays2.print(a3, size/3, size/3 + size/3);
Arrays2.fill(a4,
new Arrays2.RandShortGenerator());
Arrays2.print(a4);
Arrays2.print("a4 = ", a4);
Arrays2.print(a4, size/3, size/3 + size/3);
Arrays2.fill(a5,
new Arrays2.RandIntGenerator());
Arrays2.print(a5);
Arrays2.print("a5 = ", a5);
Arrays2.print(a5, size/3, size/3 + size/3);
Arrays2.fill(a6,
new Arrays2.RandLongGenerator());
Arrays2.print(a6);
Arrays2.print("a6 = ", a6);
Arrays2.print(a6, size/3, size/3 + size/3);
Arrays2.fill(a7,
new Arrays2.RandFloatGenerator());
Arrays2.print(a7);
Arrays2.print("a7 = ", a7);
Arrays2.print(a7, size/3, size/3 + size/3);
Arrays2.fill(a8,
new Arrays2.RandDoubleGenerator());
Arrays2.print(a8);
Arrays2.print("a8 = ", a8);
Arrays2.print(a8, size/3, size/3 + size/3);
Arrays2.fill(a9,
new Arrays2.RandStringGenerator(7));
Arrays2.print(a9);
Arrays2.print("a9 = ", a9);
Arrays2.print(a9, size/3, size/3 + size/3);
}
} ///:~The Java standard library Arrays
also has a fill( ) method, but that is rather trivial—it only
duplicates a single value into each location, or in the case of objects, copies
the same reference into each location. Using Arrays2.print( ), the
Arrays.fill( ) methods can be easily
demonstrated:
//: c09:FillingArrays.java
// Using Arrays.fill()
import com.bruceeckel.util.*;
import java.util.*;
public class FillingArrays {
public static void main(String[] args) {
int size = 6;
// Or get the size from the command line:
if(args.length != 0)
size = Integer.parseInt(args[0]);
boolean[] a1 = new boolean[size];
byte[] a2 = new byte[size];
char[] a3 = new char[size];
short[] a4 = new short[size];
int[] a5 = new int[size];
long[] a6 = new long[size];
float[] a7 = new float[size];
double[] a8 = new double[size];
String[] a9 = new String[size];
Arrays.fill(a1, true);
Arrays2.print("a1 = ", a1);
Arrays.fill(a2, (byte)11);
Arrays2.print("a2 = ", a2);
Arrays.fill(a3, 'x');
Arrays2.print("a3 = ", a3);
Arrays.fill(a4, (short)17);
Arrays2.print("a4 = ", a4);
Arrays.fill(a5, 19);
Arrays2.print("a5 = ", a5);
Arrays.fill(a6, 23);
Arrays2.print("a6 = ", a6);
Arrays.fill(a7, 29);
Arrays2.print("a7 = ", a7);
Arrays.fill(a8, 47);
Arrays2.print("a8 = ", a8);
Arrays.fill(a9, "Hello");
Arrays2.print("a9 = ", a9);
// Manipulating ranges:
Arrays.fill(a9, 3, 5, "World");
Arrays2.print("a9 = ", a9);
}
} ///:~You can either fill the entire array,
or—as the last two statements show—a range of elements. But since
you can only provide a single value to use for filling using
Arrays.fill( ), the Arrays2.fill( ) methods produce much
more interesting results.
The Java standard library provides a
static method, System.arraycopy( ),
which can make much faster copies of an array than if you use a for loop
to perform the copy by hand. System.arraycopy( ) is overloaded to
handle all types. Here’s an example that manipulates arrays of
int:
//: c09:CopyingArrays.java
// Using System.arraycopy()
import com.bruceeckel.util.*;
import java.util.*;
public class CopyingArrays {
public static void main(String[] args) {
int[] i = new int[25];
int[] j = new int[25];
Arrays.fill(i, 47);
Arrays.fill(j, 99);
Arrays2.print("i = ", i);
Arrays2.print("j = ", j);
System.arraycopy(i, 0, j, 0, i.length);
Arrays2.print("j = ", j);
int[] k = new int[10];
Arrays.fill(k, 103);
System.arraycopy(i, 0, k, 0, k.length);
Arrays2.print("k = ", k);
Arrays.fill(k, 103);
System.arraycopy(k, 0, i, 0, k.length);
Arrays2.print("i = ", i);
// Objects:
Integer[] u = new Integer[10];
Integer[] v = new Integer[5];
Arrays.fill(u, new Integer(47));
Arrays.fill(v, new Integer(99));
Arrays2.print("u = ", u);
Arrays2.print("v = ", v);
System.arraycopy(v, 0,
u, u.length/2, v.length);
Arrays2.print("u = ", u);
}
} ///:~The arguments to arraycopy( )
are the source array, the offset into the source array from whence to start
copying, the destination array, the offset into the destination array where the
copying begins, and the number of elements to copy. Naturally, any violation of
the array boundaries will cause an exception.
The example shows that both primitive
arrays and object arrays can be copied. However, if you copy arrays of objects
then only the references get copied—there’s no duplication of the
objects themselves. This is called a shallow copy (see Appendix
A).
Arrays provides the overloaded
method equals( ) to compare entire arrays for equality. Again, these
are overloaded for all the primitives, and for Object. To be equal, the
arrays must have the same number of elements and each element must be equivalent
to each corresponding element in the other array, using the equals( )
for each element. (For primitives, that primitive’s wrapper class
equals( ) is used; for example, Integer.equals( ) for
int.) Here’s an example:
//: c09:ComparingArrays.java
// Using Arrays.equals()
import java.util.*;
public class ComparingArrays {
public static void main(String[] args) {
int[] a1 = new int[10];
int[] a2 = new int[10];
Arrays.fill(a1, 47);
Arrays.fill(a2, 47);
System.out.println(Arrays.equals(a1, a2));
a2[3] = 11;
System.out.println(Arrays.equals(a1, a2));
String[] s1 = new String[5];
Arrays.fill(s1, "Hi");
String[] s2 = {"Hi", "Hi", "Hi", "Hi", "Hi"};
System.out.println(Arrays.equals(s1, s2));
}
} ///:~Originally, a1 and a2 are
exactly equal, so the output is “true,” but then one of the elements
is changed so the second line of output is “false.” In the last
case, all the elements of s1 point to the same object, but s2 has
five unique objects. However, array equality is based on contents (via
Object.equals( )) and so the result is
“true.”
One of the missing features in the Java
1.0 and 1.1 libraries is algorithmic operations—even simple
sorting. This was a rather confusing situation to someone
expecting an adequate standard library. Fortunately, Java 2 remedies the
situation, at least for the sorting problem.
A problem with writing generic sorting
code is that sorting must perform comparisons based on the actual type of the
object. Of course, one approach is to write a different sorting method for every
different type, but you should be able to recognize that this does not produce
code that is easily reused for new types.
A primary goal of programming design is
to “separate things that change from things that stay the same,” and
here, the code that stays the same is the general sort algorithm, but the thing
that changes from one use to the next is the way objects are compared. So
instead of hard-wiring the comparison code into many different sort routines,
the technique of the callback is used. With a
callback, the part of the code that varies from case to case is encapsulated
inside its own class, and the part of the code that’s always the same will
call back to the code that changes. That way you can make different objects to
express different ways of comparison and feed them to the same sorting
code.
In Java 2, there are two ways to provide
comparison functionality. The first is with the natural comparison method
that is imparted to a class by implementing the java.lang.Comparable
interface. This is a very simple interface with a single method,
compareTo( ). This method takes another
Object as an argument, and produces a negative value if the argument is
less than the current object, zero if the argument is equal, and a positive
value if the argument is greater than the current object.
Here’s a class that implements
Comparable and demonstrates the comparability by
using the Java standard library method
Arrays.sort( ):
//: c09:CompType.java
// Implementing Comparable in a class.
import com.bruceeckel.util.*;
import java.util.*;
public class CompType implements Comparable {
int i;
int j;
public CompType(int n1, int n2) {
i = n1;
j = n2;
}
public String toString() {
return "[i = " + i + ", j = " + j + "]";
}
public int compareTo(Object rv) {
int rvi = ((CompType)rv).i;
return (i < rvi ? -1 : (i == rvi ? 0 : 1));
}
private static Random r = new Random();
private static int randInt() {
return Math.abs(r.nextInt()) % 100;
}
public static Generator generator() {
return new Generator() {
public Object next() {
return new CompType(randInt(),randInt());
}
};
}
public static void main(String[] args) {
CompType[] a = new CompType[10];
Arrays2.fill(a, generator());
Arrays2.print("before sorting, a = ", a);
Arrays.sort(a);
Arrays2.print("after sorting, a = ", a);
}
} ///:~When you define the comparison function,
you are responsible for deciding what it means to compare one of your objects to
another. Here, only the i values are used in the comparison, and the
j values are ignored.
The static randInt( ) method
produces positive values between zero and 100, and the generator( )
method produces an object that implements the Generator interface, by
creating an anonymous inner class (see Chapter 8). This builds CompType
objects by initializing them with random values. In main( ), the
generator is used to fill an array of CompType, which is then sorted. If
Comparable hadn’t been implemented, then you’d get a
compile-time error message when you tried to call
sort( ).
Now suppose someone hands you a class
that doesn’t implement Comparable, or they hand you this class that
does implement Comparable, but you decide you don’t like the
way it works and would rather have a different comparison function for the type.
To do this, you use the second approach for comparing objects, by creating a
separate class that implements an interface called
Comparator. This has two methods,
compare( ) and equals( ). However, you don’t have
to implement equals( ) except for special performance needs, because
anytime you create a class it is implicitly inherited from Object, which
has an equals( ). So you can just use the default Object
equals( ) and satisfy the contract imposed by the
interface.
The Collections class (which
we’ll look at more later) contains a single Comparator that
reverses the natural sorting order. This can easily be applied to the
CompType:
//: c09:Reverse.java
// The Collecions.reverseOrder() Comparator.
import com.bruceeckel.util.*;
import java.util.*;
public class Reverse {
public static void main(String[] args) {
CompType[] a = new CompType[10];
Arrays2.fill(a, CompType.generator());
Arrays2.print("before sorting, a = ", a);
Arrays.sort(a, Collections.reverseOrder());
Arrays2.print("after sorting, a = ", a);
}
} ///:~As a second example, the following
Comparator compares CompType objects based on their j
values rather than their i values:
//: c09:ComparatorTest.java
// Implementing a Comparator for a class.
import com.bruceeckel.util.*;
import java.util.*;
class CompTypeComparator implements Comparator {
public int compare(Object o1, Object o2) {
int j1 = ((CompType)o1).j;
int j2 = ((CompType)o2).j;
return (j1 < j2 ? -1 : (j1 == j2 ? 0 : 1));
}
}
public class ComparatorTest {
public static void main(String[] args) {
CompType[] a = new CompType[10];
Arrays2.fill(a, CompType.generator());
Arrays2.print("before sorting, a = ", a);
Arrays.sort(a, new CompTypeComparator());
Arrays2.print("after sorting, a = ", a);
}
} ///:~The compare( ) method must
return a negative integer, zero, or a positive integer if the first argument is
less than, equal to, or greater than the second,
respectively.
With the built-in sorting methods, you
can sort any array of primitives, and any array of objects that either
implements Comparable or has an associated Comparator. This fills
a big hole in the Java libraries—believe it or not, there was no support
in Java 1.0 or 1.1 for sorting Strings! Here’s an example that
generates random String objects and sorts them:
//: c09:StringSorting.java
// Sorting an array of Strings.
import com.bruceeckel.util.*;
import java.util.*;
public class StringSorting {
public static void main(String[] args) {
String[] sa = new String[30];
Arrays2.fill(sa,
new Arrays2.RandStringGenerator(5));
Arrays2.print("Before sorting: ", sa);
Arrays.sort(sa);
Arrays2.print("After sorting: ", sa);
}
} ///:~One thing you’ll notice about the
output in the String sorting algorithm is that it’s
lexicographic,
so it puts all the words starting with uppercase letters first, followed by all
the words starting with lowercase letters. (Telephone books are typically sorted
this way.) You may also want to group the words together regardless of case, and
you can do this by defining a Comparator class, thereby overriding the
default String Comparable behavior. For reuse, this will be added to the
“util” package:
//: com:bruceeckel:util:AlphabeticComparator.java
// Keeping upper and lowercase letters together.
package com.bruceeckel.util;
import java.util.*;
public class AlphabeticComparator
implements Comparator{
public int compare(Object o1, Object o2) {
String s1 = (String)o1;
String s2 = (String)o2;
return s1.toLowerCase().compareTo(
s2.toLowerCase());
}
} ///:~Each String is converted to
lowercase before the comparison. String’s built-in
compareTo( ) method provides the desired
functionality.
Here’s a test using
AlphabeticComparator:
//: c09:AlphabeticSorting.java
// Keeping upper and lowercase letters together.
import com.bruceeckel.util.*;
import java.util.*;
public class AlphabeticSorting {
public static void main(String[] args) {
String[] sa = new String[30];
Arrays2.fill(sa,
new Arrays2.RandStringGenerator(5));
Arrays2.print("Before sorting: ", sa);
Arrays.sort(sa, new AlphabeticComparator());
Arrays2.print("After sorting: ", sa);
}
} ///:~The sorting algorithm that’s used
in the Java standard library is designed to be optimal for the particular type
you’re sorting—a Quicksort for primitives, and a stable merge sort
for objects. So you shouldn’t need to spend any time worrying about
performance unless your profiling tool points you to the sorting process as a
bottleneck.
Once an array is sorted, you can perform
a fast search for a particular item using
Arrays.binarySearch( ). However, it’s
very important that you do not try to use
binarySearch( ) on an unsorted array; the
results will be unpredictable. The following example uses a
RandIntGenerator to fill an array, then to produces values to search
for:
//: c09:ArraySearching.java
// Using Arrays.binarySearch().
import com.bruceeckel.util.*;
import java.util.*;
public class ArraySearching {
public static void main(String[] args) {
int[] a = new int[100];
Arrays2.RandIntGenerator gen =
new Arrays2.RandIntGenerator(1000);
Arrays2.fill(a, gen);
Arrays.sort(a);
Arrays2.print("Sorted array: ", a);
while(true) {
int r = gen.next();
int location = Arrays.binarySearch(a, r);
if(location >= 0) {
System.out.println("Location of " + r +
" is " + location + ", a[" +
location + "] = " + a[location]);
break; // Out of while loop
}
}
}
} ///:~In the while loop, random values
are generated as search items, until one of them is found.
Arrays.binarySearch( )
produces a value greater than or equal to zero if the search item is found.
Otherwise, it produces a negative value representing the place that the element
should be inserted if you are maintaining the sorted array by hand. The value
produced is
-(insertion point) - 1
The insertion point is the index of the
first element greater than the key, or a.size( ), if all elements in
the array are less than the specified key.
If the array contains duplicate elements,
there is no guarantee which one will be found. The algorithm is thus not really
designed to support duplicate elements, as much as tolerate them. If you need a
sorted list of nonduplicated elements, however, use a TreeSet, which will
be introduced later in this chapter. This takes care of all the details for you
automatically. Only in cases of performance bottlenecks should you replace the
TreeSet with a hand-maintained array.
If you have sorted an object array using
a Comparator (primitive arrays do not allow sorting with a
Comparator), you must include that same Comparator when you
perform a binarySearch( ) (using the overloaded version of the
function that’s provided). For example, the AlphabeticSorting.java
program can be modified to perform a search:
//: c09:AlphabeticSearch.java
// Searching with a Comparator.
import com.bruceeckel.util.*;
import java.util.*;
public class AlphabeticSearch {
public static void main(String[] args) {
String[] sa = new String[30];
Arrays2.fill(sa,
new Arrays2.RandStringGenerator(5));
AlphabeticComparator comp =
new AlphabeticComparator();
Arrays.sort(sa, comp);
int index =
Arrays.binarySearch(sa, sa[10], comp);
System.out.println("Index = " + index);
}
} ///:~The Comparator must be passed to
the overloaded binarySearch( ) as the third argument. In the above
example, success is guaranteed because the search item is plucked out of the
array itself.
To summarize what you’ve seen so
far, your first and most efficient choice to hold a group of objects should be
an array, and you’re forced into this choice if you want to hold a group
of primitives. In the remainder of this chapter we’ll look at the more
general case, when you don’t know at the time you’re writing the
program how many objects you’re going to need, or if you need a more
sophisticated way to store your objects. Java provides a library of
container classes to solve this problem, the basic
types of which are List,
Set, and Map.
You can solve a surprising number of problems using these
tools.
Among their other
characteristics—Set, for example, holds only one object of each
value, and Map is an associative array that
lets you associate any object with any other object—the Java container
classes will automatically resize themselves. So, unlike arrays, you can put in
any number of objects and you don’t need to worry about how big to make
the container while you’re writing the
program.
To me, container classes are one of the
most powerful tools for raw development because they significantly increase your
programming muscle. The Java 2
containers represent a thorough
redesign[48] of the
rather poor showings in Java 1.0 and 1.1. Some of the redesign makes things
tighter and more sensible. It also fills out the functionality of the containers
library, providing the behavior of linked lists,
queues, and deques (double-ended
queues, pronounced “decks”).
The design of a containers library is
difficult (true of most library design problems). In
C++, the container classes covered
the bases with many different classes. This was better than what was available
prior to the C++ container classes (nothing), but it didn’t translate well
into Java. On the other extreme, I’ve seen a containers library that
consists of a single class, “container,” which acts like both a
linear sequence and an associative array at the same time. The Java 2 container
library strikes a balance: the full functionality that you expect from a mature
container library, but easier to learn and use than the C++ container classes
and other similar container libraries. The result can seem a bit odd in places.
Unlike some of the decisions made in the early Java libraries, these oddities
were not accidents, but carefully considered decisions based on trade-offs in
complexity. It might take you a little while to get comfortable with some
aspects of the library, but I think you’ll find yourself rapidly acquiring
and using these new tools.
The Java 2 container library takes the
issue of “holding your objects” and divides it into two distinct
concepts:
We will first look at
the general features of containers, then go into details, and finally learn why
there are different versions of some containers, and how to choose between
them.
Unlike arrays, the containers print
nicely without any help. Here’s an example that also introduces you to the
basic types of containers:
//: c09:PrintingContainers.java
// Containers print themselves automatically.
import java.util.*;
public class PrintingContainers {
static Collection fill(Collection c) {
c.add("dog");
c.add("dog");
c.add("cat");
return c;
}
static Map mfill(Map m) {
m.put("dog", "Bosco");
m.put("dog", "Spot");
m.put("cat", "Rags");
return m;
}
public static void main(String[] args) {
System.out.println(fill(new ArrayList()));
System.out.println(fill(new HashSet()));
System.out.println(mfill(new HashMap()));
}
} ///:~As mentioned before, there are two basic
categories in the Java container library. The distinction is based on the number
of items that are held in each location of the container. The Collection
category only holds one item in each location (the name is a bit misleading
since entire container libraries are often called “collections”). It
includes the List, which holds a group of items in a specified sequence,
and the Set, which only allows the addition of one item of each type. The
ArrayList is a type of List, and HashSet is a type of
Set. To add items to any Collection, there’s an
add( ) method.
The Map holds key-value pairs,
rather like a mini database. The above program uses one flavor of Map,
the HashMap. If you have a Map that associates states with
their capitals and you want to know the capital of Ohio, you look it
up—almost as if you were indexing into an array. (Maps are also called
associative arrays.) To add
elements to a Map there’s a put( ) method that takes a
key and a value as arguments. The above example only shows adding elements and
does not look the elements up after they’re added. That will be shown
later.
The fill( ) and
mfill( ) methods fill Collections and Maps,
respectively. If you look at the output, you can see that the default printing
behavior (provided via the container’s various toString( )
methods) produces quite readable results, so no additional printing support is
necessary as it was with arrays:
[dog, dog, cat]
[cat, dog]
{cat=Rags, dog=Spot}A Collection is printed surrounded
by square braces, with each element separated by a comma. A Map is
surrounded by curly braces, with each key and value associated with an equal
sign (keys on the left, values on the right).
You can also immediately see the basic
behavior of the different containers. The List holds the objects exactly
as they are entered, without any reordering or editing. The Set, however,
only accepts one of each object and it uses its own internal ordering method (in
general, you are only concerned with whether or not something is a member of the
Set, not the order in which it appears—for that you’d use a
List). And the Map also only accepts one of each type of item,
based on the key, and it also has its own internal ordering and does not care
about the order in which you enter the
items.
Although the problem of printing the
containers is taken care of, filling containers suffers from the same deficiency
as java.util.Arrays. Just like Arrays, there is a companion class
called Collections containing static utility methods including one
called fill( ). This fill( ) also
just duplicates a single object reference throughout the container, and also
only works for List objects and not Sets or
Maps:
//: c09:FillingLists.java
// The Collections.fill() method.
import java.util.*;
public class FillingLists {
public static void main(String[] args) {
List list = new ArrayList();
for(int i = 0; i < 10; i++)
list.add("");
Collections.fill(list, "Hello");
System.out.println(list);
}
} ///:~This method is made even less useful by
the fact that it can only replace elements that are already in the List,
and will not add new elements.
To be able to create interesting
examples, here is a complementary Collections2 library (part of
com.bruceeckel.util for convenience) with a fill( ) method
that uses a generator to add elements, and allows you to
specify the number of elements you want to add( ). The Generator
interface defined previously will work for Collections, but the
Map requires its own generator interface since a pair of objects
(one key and one value) must be produced by each call to next( ).
Here is the Pair class:
//: com:bruceeckel:util:Pair.java
package com.bruceeckel.util;
public class Pair {
public Object key, value;
Pair(Object k, Object v) {
key = k;
value = v;
}
} ///:~Next, the generator interface that
produces the Pair:
//: com:bruceeckel:util:MapGenerator.java
package com.bruceeckel.util;
public interface MapGenerator {
Pair next();
} ///:~//: com:bruceeckel:util:Collections2.java
// To fill any type of container
// using a generator object.
package com.bruceeckel.util;
import java.util.*;
public class Collections2 {
// Fill an array using a generator:
public static void
fill(Collection c, Generator gen, int count) {
for(int i = 0; i < count; i++)
c.add(gen.next());
}
public static void
fill(Map m, MapGenerator gen, int count) {
for(int i = 0; i < count; i++) {
Pair p = gen.next();
m.put(p.key, p.value);
}
}
public static class RandStringPairGenerator
implements MapGenerator {
private Arrays2.RandStringGenerator gen;
public RandStringPairGenerator(int len) {
gen = new Arrays2.RandStringGenerator(len);
}
public Pair next() {
return new Pair(gen.next(), gen.next());
}
}
// Default object so you don't have
// to create your own:
public static RandStringPairGenerator rsp =
new RandStringPairGenerator(10);
public static class StringPairGenerator
implements MapGenerator {
private int index = -1;
private String[][] d;
public StringPairGenerator(String[][] data) {
d = data;
}
public Pair next() {
// Force the index to wrap:
index = (index + 1) % d.length;
return new Pair(d[index][0], d[index][1]);
}
public StringPairGenerator reset() {
index = -1;
return this;
}
}
// Use a predefined dataset:
public static StringPairGenerator geography =
new StringPairGenerator(
CountryCapitals.pairs);
// Produce a sequence from a 2D array:
public static class StringGenerator
implements Generator {
private String[][] d;
private int position;
private int index = -1;
public
StringGenerator(String[][] data, int pos) {
d = data;
position = pos;
}
public Object next() {
// Force the index to wrap:
index = (index + 1) % d.length;
return d[index][position];
}
public StringGenerator reset() {
index = -1;
return this;
}
}
// Use a predefined dataset:
public static StringGenerator countries =
new StringGenerator(CountryCapitals.pairs,0);
public static StringGenerator capitals =
new StringGenerator(CountryCapitals.pairs,1);
} ///:~Both versions of fill( ) take
an argument that determines the number of items to add to the container. In
addition, there are two generators for the map: RandStringPairGenerator,
which creates any number of pairs of gibberish Strings with length
determined by the constructor argument; and StringPairGenerator, which
produces pairs of Strings given a two-dimensional array of String.
The StringGenerator also takes a two-dimensional array of String
but generates single items rather than Pairs. The static
rsp, geography, countries, and capitals objects provide
prebuilt generators, the last three using all the countries of the world
and their capitals. Note that if you try to create more pairs than are
available, the generators will loop around to the beginning, and if you are
putting the pairs into a Map, the duplicates will just be
ignored.
Here is the predefined dataset, which
consists of country names and their capitals. It is set in a small font to
prevent taking up unnecessary space:
//: com:bruceeckel:util:CountryCapitals.java
package com.bruceeckel.util;
public class CountryCapitals {
public static final String[][] pairs = {
// Africa
{"ALGERIA","Algiers"}, {"ANGOLA","Luanda"},
{"BENIN","Porto-Novo"}, {"BOTSWANA","Gaberone"},
{"BURKINA FASO","Ouagadougou"}, {"BURUNDI","Bujumbura"},
{"CAMEROON","Yaounde"}, {"CAPE VERDE","Praia"},
{"CENTRAL AFRICAN REPUBLIC","Bangui"},
{"CHAD","N'djamena"}, {"COMOROS","Moroni"},
{"CONGO","Brazzaville"}, {"DJIBOUTI","Dijibouti"},
{"EGYPT","Cairo"}, {"EQUATORIAL GUINEA","Malabo"},
{"ERITREA","Asmara"}, {"ETHIOPIA","Addis Ababa"},
{"GABON","Libreville"}, {"THE GAMBIA","Banjul"},
{"GHANA","Accra"}, {"GUINEA","Conakry"},
{"GUINEA","-"}, {"BISSAU","Bissau"},
{"CETE D'IVOIR (IVORY COAST)","Yamoussoukro"},
{"KENYA","Nairobi"}, {"LESOTHO","Maseru"},
{"LIBERIA","Monrovia"}, {"LIBYA","Tripoli"},
{"MADAGASCAR","Antananarivo"}, {"MALAWI","Lilongwe"},
{"MALI","Bamako"}, {"MAURITANIA","Nouakchott"},
{"MAURITIUS","Port Louis"}, {"MOROCCO","Rabat"},
{"MOZAMBIQUE","Maputo"}, {"NAMIBIA","Windhoek"},
{"NIGER","Niamey"}, {"NIGERIA","Abuja"},
{"RWANDA","Kigali"}, {"SAO TOME E PRINCIPE","Sao Tome"},
{"SENEGAL","Dakar"}, {"SEYCHELLES","Victoria"},
{"SIERRA LEONE","Freetown"}, {"SOMALIA","Mogadishu"},
{"SOUTH AFRICA","Pretoria/Cape Town"}, {"SUDAN","Khartoum"},
{"SWAZILAND","Mbabane"}, {"TANZANIA","Dodoma"},
{"TOGO","Lome"}, {"TUNISIA","Tunis"},
{"UGANDA","Kampala"},
{"DEMOCRATIC REPUBLIC OF THE CONGO (ZAIRE)","Kinshasa"},
{"ZAMBIA","Lusaka"}, {"ZIMBABWE","Harare"},
// Asia
{"AFGHANISTAN","Kabul"}, {"BAHRAIN","Manama"},
{"BANGLADESH","Dhaka"}, {"BHUTAN","Thimphu"},
{"BRUNEI","Bandar Seri Begawan"}, {"CAMBODIA","Phnom Penh"},
{"CHINA","Beijing"}, {"CYPRUS","Nicosia"},
{"INDIA","New Delhi"}, {"INDONESIA","Jakarta"},
{"IRAN","Tehran"}, {"IRAQ","Baghdad"},
{"ISRAEL","Jerusalem"}, {"JAPAN","Tokyo"},
{"JORDAN","Amman"}, {"KUWAIT","Kuwait City"},
{"LAOS","Vientiane"}, {"LEBANON","Beirut"},
{"MALAYSIA","Kuala Lumpur"}, {"THE MALDIVES","Male"},
{"MONGOLIA","Ulan Bator"}, {"MYANMAR (BURMA)","Rangoon"},
{"NEPAL","Katmandu"}, {"NORTH KOREA","P'yongyang"},
{"OMAN","Muscat"}, {"PAKISTAN","Islamabad"},
{"PHILIPPINES","Manila"}, {"QATAR","Doha"},
{"SAUDI ARABIA","Riyadh"}, {"SINGAPORE","Singapore"},
{"SOUTH KOREA","Seoul"}, {"SRI LANKA","Colombo"},
{"SYRIA","Damascus"}, {"TAIWAN (REPUBLIC OF CHINA)","Taipei"},
{"THAILAND","Bangkok"}, {"TURKEY","Ankara"},
{"UNITED ARAB EMIRATES","Abu Dhabi"}, {"VIETNAM","Hanoi"},
{"YEMEN","Sana'a"},
// Australia and Oceania
{"AUSTRALIA","Canberra"}, {"FIJI","Suva"},
{"KIRIBATI","Bairiki"},
{"MARSHALL ISLANDS","Dalap-Uliga-Darrit"},
{"MICRONESIA","Palikir"}, {"NAURU","Yaren"},
{"NEW ZEALAND","Wellington"}, {"PALAU","Koror"},
{"PAPUA NEW GUINEA","Port Moresby"},
{"SOLOMON ISLANDS","Honaira"}, {"TONGA","Nuku'alofa"},
{"TUVALU","Fongafale"}, {"VANUATU","< Port-Vila"},
{"WESTERN SAMOA","Apia"},
// Eastern Europe and former USSR
{"ARMENIA","Yerevan"}, {"AZERBAIJAN","Baku"},
{"BELARUS (BYELORUSSIA)","Minsk"}, {"GEORGIA","Tbilisi"},
{"KAZAKSTAN","Almaty"}, {"KYRGYZSTAN","Alma-Ata"},
{"MOLDOVA","Chisinau"}, {"RUSSIA","Moscow"},
{"TAJIKISTAN","Dushanbe"}, {"TURKMENISTAN","Ashkabad"},
{"UKRAINE","Kyiv"}, {"UZBEKISTAN","Tashkent"},
// Europe
{"ALBANIA","Tirana"}, {"ANDORRA","Andorra la Vella"},
{"AUSTRIA","Vienna"}, {"BELGIUM","Brussels"},
{"BOSNIA","-"}, {"HERZEGOVINA","Sarajevo"},
{"CROATIA","Zagreb"}, {"CZECH REPUBLIC","Prague"},
{"DENMARK","Copenhagen"}, {"ESTONIA","Tallinn"},
{"FINLAND","Helsinki"}, {"FRANCE","Paris"},
{"GERMANY","Berlin"}, {"GREECE","Athens"},
{"HUNGARY","Budapest"}, {"ICELAND","Reykjavik"},
{"IRELAND","Dublin"}, {"ITALY","Rome"},
{"LATVIA","Riga"}, {"LIECHTENSTEIN","Vaduz"},
{"LITHUANIA","Vilnius"}, {"LUXEMBOURG","Luxembourg"},
{"MACEDONIA","Skopje"}, {"MALTA","Valletta"},
{"MONACO","Monaco"}, {"MONTENEGRO","Podgorica"},
{"THE NETHERLANDS","Amsterdam"}, {"NORWAY","Oslo"},
{"POLAND","Warsaw"}, {"PORTUGAL","Lisbon"},
{"ROMANIA","Bucharest"}, {"SAN MARINO","San Marino"},
{"SERBIA","Belgrade"}, {"SLOVAKIA","Bratislava"},
{"SLOVENIA","Ljujiana"}, {"SPAIN","Madrid"},
{"SWEDEN","Stockholm"}, {"SWITZERLAND","Berne"},
{"UNITED KINGDOM","London"}, {"VATICAN CITY","---"},
// North and Central America
{"ANTIGUA AND BARBUDA","Saint John's"}, {"BAHAMAS","Nassau"},
{"BARBADOS","Bridgetown"}, {"BELIZE","Belmopan"},
{"CANADA","Ottawa"}, {"COSTA RICA","San Jose"},
{"CUBA","Havana"}, {"DOMINICA","Roseau"},
{"DOMINICAN REPUBLIC","Santo Domingo"},
{"EL SALVADOR","San Salvador"}, {"GRENADA","Saint George's"},
{"GUATEMALA","Guatemala City"}, {"HAITI","Port-au-Prince"},
{"HONDURAS","Tegucigalpa"}, {"JAMAICA","Kingston"},
{"MEXICO","Mexico City"}, {"NICARAGUA","Managua"},
{"PANAMA","Panama City"}, {"ST. KITTS","-"},
{"NEVIS","Basseterre"}, {"ST. LUCIA","Castries"},
{"ST. VINCENT AND THE GRENADINES","Kingstown"},
{"UNITED STATES OF AMERICA","Washington, D.C."},
// South America
{"ARGENTINA","Buenos Aires"},
{"BOLIVIA","Sucre (legal)/La Paz(administrative)"},
{"BRAZIL","Brasilia"}, {"CHILE","Santiago"},
{"COLOMBIA","Bogota"}, {"ECUADOR","Quito"},
{"GUYANA","Georgetown"}, {"PARAGUAY","Asuncion"},
{"PERU","Lima"}, {"SURINAME","Paramaribo"},
{"TRINIDAD AND TOBAGO","Port of Spain"},
{"URUGUAY","Montevideo"}, {"VENEZUELA","Caracas"},
};
} ///:~This is simply a two-dimensional array of
String
data[49].
Here’s a simple test using the fill( ) methods and
generators:
//: c09:FillTest.java
import com.bruceeckel.util.*;
import java.util.*;
public class FillTest {
static Generator sg =
new Arrays2.RandStringGenerator(7);
public static void main(String[] args) {
List list = new ArrayList();
Collections2.fill(list, sg, 25);
System.out.println(list + "\n");
List list2 = new ArrayList();
Collections2.fill(list2,
Collections2.capitals, 25);
System.out.println(list2 + "\n");
Set set = new HashSet();
Collections2.fill(set, sg, 25);
System.out.println(set + "\n");
Map m = new HashMap();
Collections2.fill(m, Collections2.rsp, 25);
System.out.println(m + "\n");
Map m2 = new HashMap();
Collections2.fill(m2,
Collections2.geography, 25);
System.out.println(m2);
}
} ///:~The “disadvantage” to using
the Java containers is that you lose type information when you put an object
into a container. This happens because the programmer of that container class
had no idea what specific type you wanted to put in the container, and making
the container hold only your type would prevent it from being a general-purpose
tool. So instead, the container holds references to Object, which is the
root of all the classes so it holds any type. (Of course, this doesn’t
include primitive types, since they aren’t inherited from anything.) This
is a great solution, except:
On the up side, Java
won’t let you misuse the objects that you put into a container. If
you throw a dog into a container of cats and then try to treat everything in the
container as a cat, you’ll get a run-time exception when you pull the dog
reference out of the cat container and try to cast it to a cat.
Here’s an example using the basic
workhorse container, ArrayList. For starters, you can think of
ArrayList as “an array that automatically expands itself.”
Using an ArrayList is straightforward: create one, put objects in using
add( ), and later get
them out with get( )
using an index—just like you would with an array but without the
square
brackets[50].
ArrayList also has a method
size( ) to let you
know how many elements have been added so you don’t inadvertently run off
the end and cause an exception.
First, Cat and Dog classes
are created:
//: c09:Cat.java
public class Cat {
private int catNumber;
Cat(int i) { catNumber = i; }
void print() {
System.out.println("Cat #" + catNumber);
}
} ///:~
//: c09:Dog.java
public class Dog {
private int dogNumber;
Dog(int i) { dogNumber = i; }
void print() {
System.out.println("Dog #" + dogNumber);
}
} ///:~Cats and Dogs are placed
into the container, then pulled out:
//: c09:CatsAndDogs.java
// Simple container example.
import java.util.*;
public class CatsAndDogs {
public static void main(String[] args) {
ArrayList cats = new ArrayList();
for(int i = 0; i < 7; i++)
cats.add(new Cat(i));
// Not a problem to add a dog to cats:
cats.add(new Dog(7));
for(int i = 0; i < cats.size(); i++)
((Cat)cats.get(i)).print();
// Dog is detected only at run-time
}
} ///:~The classes Cat and Dog are
distinct—they have nothing in common except that they are Objects.
(If you don’t explicitly say what class you’re inheriting from, you
automatically inherit from Object.) Since ArrayList holds
Objects, you can not only put Cat objects into this container
using the ArrayList method add( ), but you can also add
Dog objects without complaint at either compile-time or run-time. When
you go to fetch out what you think are Cat objects using the
ArrayList method get( ), you get back a reference to an
object that you must cast to a Cat. Then you need to surround the entire
expression with parentheses to force the evaluation of the cast before calling
the print( ) method for Cat, otherwise you’ll get a
syntax error. Then, at run-time, when you try to cast the Dog object to a
Cat, you’ll get an exception.
This is more than just an annoyance.
It’s something that can create difficult-to-find bugs. If one part (or
several parts) of a program inserts objects into a container, and you discover
only in a separate part of the program through an exception that a bad object
was placed in the container, then you must find out where the bad insert
occurred. On the upside, it’s convenient to start with some standardized
container classes for programming, despite the scarcity and
awkwardness.
It turns out that in some cases things
seem to work correctly without casting back to your original type. One case is
quite special: the String class has some extra help from the compiler to
make it work smoothly. Whenever the compiler expects a String object and
it hasn’t got one, it will automatically call the
toString( ) method
that’s defined in Object and can be overridden by any Java class.
This method produces the desired String object, which is then used
wherever it was wanted.
Thus, all you need to do to make objects
of your class print is to override the toString( ) method, as shown
in the following example:
//: c09:Mouse.java
// Overriding toString().
public class Mouse {
private int mouseNumber;
Mouse(int i) { mouseNumber = i; }
// Override Object.toString():
public String toString() {
return "This is Mouse #" + mouseNumber;
}
public int getNumber() {
return mouseNumber;
}
} ///:~
//: c09:WorksAnyway.java
// In special cases, things just
// seem to work correctly.
import java.util.*;
class MouseTrap {
static void caughtYa(Object m) {
Mouse mouse = (Mouse)m; // Cast from Object
System.out.println("Mouse: " +
mouse.getNumber());
}
}
public class WorksAnyway {
public static void main(String[] args) {
ArrayList mice = new ArrayList();
for(int i = 0; i < 3; i++)
mice.add(new Mouse(i));
for(int i = 0; i < mice.size(); i++) {
// No cast necessary, automatic
// call to Object.toString():
System.out.println(
"Free mouse: " + mice.get(i));
MouseTrap.caughtYa(mice.get(i));
}
}
} ///:~You can see toString( )
overridden in Mouse. In the second for loop in main( )
you find the statement:
System.out.println("Free mouse: " + mice.get(i));After the ‘+’ sign the
compiler expects to see a
String object.
get( ) produces an Object, so to get the desired
String the compiler implicitly calls toString( ).
Unfortunately, you can work this kind of magic only with String; it
isn’t available for any other type.
A second approach to hiding the cast has
been placed inside MouseTrap. The caughtYa( ) method accepts
not a Mouse, but an Object, which it then casts to a Mouse.
This is quite presumptuous, of course, since by accepting an Object
anything could be passed to the method. However, if the cast is
incorrect—if you passed the wrong type—you’ll get an exception
at run-time. This is not as good as compile-time checking but it’s still
robust. Note that in the use of this method:
MouseTrap.caughtYa(mice.get(i));
You might not want to give up on this
issue just yet. A more ironclad solution is to create a new class using the
ArrayList, such that it will accept only your type and produce only your
type:
//: c09:MouseList.java
// A type-conscious ArrayList.
import java.util.*;
public class MouseList {
private ArrayList list = new ArrayList();
public void add(Mouse m) {
list.add(m);
}
public Mouse get(int index) {
return (Mouse)list.get(index);
}
public int size() { return list.size(); }
} ///:~Here’s a test for the new
container:
//: c09:MouseListTest.java
public class MouseListTest {
public static void main(String[] args) {
MouseList mice = new MouseList();
for(int i = 0; i < 3; i++)
mice.add(new Mouse(i));
for(int i = 0; i < mice.size(); i++)
MouseTrap.caughtYa(mice.get(i));
}
} ///:~This is similar to the previous example,
except that the new MouseList class has a private member of type
ArrayList, and methods just like ArrayList. However, it
doesn’t accept and produce generic Objects, only Mouse
objects.
Note that if MouseList had instead
been inherited from ArrayList, the add(Mouse) method would
simply overload the existing add(Object) and there would still be no
restriction on what type of objects could be added. Thus, the MouseList
becomes a surrogate to the ArrayList, performing some activities
before passing on the responsibility (see Thinking in Patterns with Java,
downloadable at www.BruceEckel.com).
Because a MouseList will accept
only a Mouse, if you say:
mice.add(new Pigeon());
you will get an error message at
compile-time. This approach, while more tedious from a coding standpoint,
will tell you immediately if you’re using a type
improperly.
Note that no cast is necessary when using
get( )—it’s always a Mouse.
This kind of problem isn’t
isolated—there are numerous cases in which you need to create new types
based on other types, and in which it is useful to have specific type
information at compile-time. This is the concept of a
parameterized type. In C++,
this is directly supported by the language with
templates. It is likely
that a future version of Java will support some variation of parameterized
types; the current front-runner automatically creates classes similar to
MouseList.
In any container class, you must have a
way to put things in and a way to get things out. After all, that’s the
primary job of a container—to hold things. In the
ArrayList, add( ) is the way that you
insert objects, and get( ) is one way to get things out.
ArrayList is quite flexible—you can select anything at any time,
and select multiple elements at once using different
indexes.
If you want to start thinking at a higher
level, there’s a drawback: you need to know the exact type of the
container in order to use it. This might not seem bad at first, but what if you
start out using an ArrayList, and later on in your program you discover
that because of the way you are using the container it would be much more
efficient to use a LinkedList instead? Or suppose you’d like to
write a piece of generic code that doesn’t know or care what type of
container it’s working with, so that it could be used on different types
of containers without rewriting that code?
The concept of an
iterator can be used to achieve this abstraction.
An iterator is an object whose job is to move through a sequence of objects and
select each object in that sequence without the client programmer knowing or
caring about the underlying structure of that sequence. In addition, an iterator
is usually what’s called a “light-weight” object: one
that’s cheap to create. For that reason, you’ll often find seemingly
strange constraints for iterators; for example, some iterators can move in only
one direction.
The Java Iterator is an example of
an iterator with these kinds of constraints. There’s not much you can do
with one except:
That’s
all. It’s a simple implementation of an iterator, but still powerful (and
there’s a more sophisticated ListIterator for Lists). To see
how it works, let’s revisit the CatsAndDogs.java program from
earlier in this chapter. In the original version, the method get( )
was used to select each element, but in the following modified version an
Iterator is used:
//: c09:CatsAndDogs2.java
// Simple container with Iterator.
import java.util.*;
public class CatsAndDogs2 {
public static void main(String[] args) {
ArrayList cats = new ArrayList();
for(int i = 0; i < 7; i++)
cats.add(new Cat(i));
cats.add(new Dog(7));
Iterator e = cats.iterator();
while(e.hasNext())
((Cat)e.next()).print();
}
} ///:~You can see that the only change is in
the last few lines, where an Iterator is used to step through the
sequence instead of a for loop. With the Iterator, you don’t
need to worry about the number of elements in the container. That’s taken
care of for you by
hasNext( ) and
next( ).
As another example, consider the creation
of a general-purpose printing method:
//: c09:HamsterMaze.java
// Using an Iterator.
import java.util.*;
class Hamster {
private int hamsterNumber;
Hamster(int i) { hamsterNumber = i; }
public String toString() {
return "This is Hamster #" + hamsterNumber;
}
}
class Printer {
static void printAll(Iterator e) {
while(e.hasNext())
System.out.println(e.next());
}
}
public class HamsterMaze {
public static void main(String[] args) {
ArrayList v = new ArrayList();
for(int i = 0; i < 3; i++)
v.add(new Hamster(i));
Printer.printAll(v.iterator());
}
} ///:~Look closely at printAll( ).
Note that there’s no information about the type of sequence. All you have
is an Iterator, and that’s all you need to know about the sequence:
that you can get the next object, and that you can know when you’re at the
end. This idea of taking a container of objects and passing through it to
perform an operation on each one is powerful, and will be seen throughout this
book.
The
example is even more generic, since it implicitly uses the
Object.toString( ) method. The println( ) method is
overloaded for all the primitive types as well as Object; in each case a
String is automatically produced by calling the appropriate
toString( ) method.
Although it’s unnecessary, you can
be more explicit using a cast, which has the effect of calling
toString( ):
System.out.println((String)e.next());
In general, however, you’ll want to
do something more than call Object methods, so you’ll run up
against the type-casting issue again. You must assume you’ve gotten an
Iterator to a sequence of the particular type you’re interested in,
and cast the resulting objects to that type (getting a run-time exception if
you’re wrong).
Because (like every other class),
the Java standard containers are inherited from
Object, they contain a toString( ) method. This has
been overridden so that they can produce a String representation of
themselves, including the objects they hold. Inside ArrayList, for
example, the toString( ) steps through the elements of the
ArrayList and calls toString( ) for each one. Suppose
you’d like to print the address of your class. It seems to make sense to
simply refer to this (in particular, C++ programmers are prone to this
approach):
//: c09:InfiniteRecursion.java
// Accidental recursion.
import java.util.*;
public class InfiniteRecursion {
public String toString() {
return " InfiniteRecursion address: "
+ this + "\n";
}
public static void main(String[] args) {
ArrayList v = new ArrayList();
for(int i = 0; i < 10; i++)
v.add(new InfiniteRecursion());
System.out.println(v);
}
} ///:~If you simply create an
InfiniteRecursion object and then print it, you’ll get an endless
sequence of exceptions. This is also true if you place the
InfiniteRecursion objects in an ArrayList and print that
ArrayList as shown here. What’s happening is automatic type
conversion for Strings. When you say:
"InfiniteRecursion address: " + this
The compiler sees a String
followed by a ‘+’ and something that’s not a
String, so it tries to convert this to a String. It does
this conversion by calling toString( ), which produces a
recursive call.
If you really do want to print the
address of the object in this case, the solution is to call the Object
toString( ) method, which does just that. So instead of saying
this, you’d say super.toString( ). (This only works if
you're directly inheriting from Object, or if none of your parent classes
have overridden the toString( )
method.)
Collections and Maps may be
implemented in different ways, according to your programming needs. It’s
helpful to look at a diagram of the Java 2 containers:
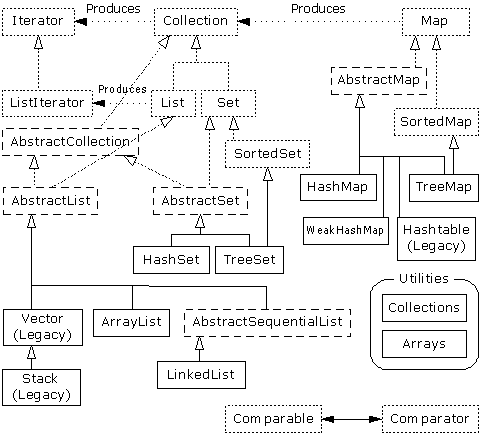
This diagram can be a bit overwhelming at
first, but you’ll see that there are really only three container
components: Map, List, and Set, and only two or three
implementations of each one (with, typically, a preferred version). When you see
this, the containers are not so daunting.
The dotted boxes represent
interfaces, the dashed boxes represent abstract classes, and the
solid boxes are regular (concrete) classes. The dotted-line arrows indicate that
a particular class is implementing an interface (or in the case of an
abstract class, partially implementing that interface). The solid
arrows show that a class can produce objects of the class the arrow is pointing
to. For example, any Collection can produce an Iterator, while a
List can produce a ListIterator (as well as an ordinary
Iterator, since List is inherited from
Collection).
The interfaces that are concerned with
holding objects are Collection, List, Set, and
Map. Ideally, you’ll write most of your code to talk to
these interfaces, and the only place where you’ll specify the precise type
you’re using is at the point of creation. So you can create a List
like this:
List x = new LinkedList();
Of course, you can also decide to make
x a LinkedList (instead of a generic List) and carry
the precise type information around with x. The beauty (and the intent)
of using the interface is that if you decide you want to change your
implementation, all you need to do is change it at the point of creation, like
this:
List x = new ArrayList();
The rest of your code can remain
untouched (some of this genericity can also be achieved with
iterators).
In the class hierarchy, you can see a
number of classes whose names begin with “Abstract,” and
these can seem a bit confusing at first. They are simply tools that partially
implement a particular interface. If you were making your own Set, for
example, you wouldn’t start with the Set interface and implement
all the methods, instead you’d inherit from
AbstractSet and do the minimal necessary work to
make your new class. However, the containers library contains enough
functionality to satisfy your needs virtually all the time. So for our purposes,
you can ignore any class that begins with
“Abstract.”
Therefore, when you look at the diagram,
you’re really concerned with only those interfaces at the top of
the diagram and the concrete classes (those with solid boxes around them).
You’ll typically make an object of a concrete class, upcast it to the
corresponding interface, and then use the interface throughout the
rest of your code. In addition, you do not need to consider the legacy elements
when writing new code. Therefore, the diagram can be greatly simplified to look
like this:
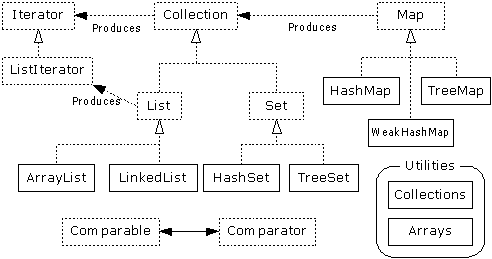
Now it only includes the interfaces and
classes that you will encounter on a regular basis, and also the elements that
we will focus on in this chapter.
Here’s a simple example, which
fills a Collection (represented here with an ArrayList) with
String objects, and then prints each element in the
Collection:
//: c09:SimpleCollection.java
// A simple example using Java 2 Collections.
import java.util.*;
public class SimpleCollection {
public static void main(String[] args) {
// Upcast because we just want to
// work with Collection features
Collection c = new ArrayList();
for(int i = 0; i < 10; i++)
c.add(Integer.toString(i));
Iterator it = c.iterator();
while(it.hasNext())
System.out.println(it.next());
}
} ///:~The first line in main( )
creates an ArrayList object and then upcasts it to
a Collection. Since this example uses only the Collection methods,
any object of a class inherited from Collection would work, but
ArrayList is the typical workhorse Collection.
The add( ) method, as its
name suggests, puts a new element in the Collection. However, the
documentation carefully states that add( ) “ensures that this
Container contains the specified element.” This is to allow for the
meaning of Set, which adds the element only if it isn’t already
there. With an ArrayList, or any sort of List, add( )
always means “put it in,” because Lists don’t care if
there are duplicates.
All Collections can produce an
Iterator via their
iterator( ) method. Here, an Iterator
is created and used to traverse the Collection, printing each
element.
The following table shows everything you
can do with a Collection (not including the methods that automatically
come through with Object), and thus, everything you can do with a
Set or a List. (List also has additional functionality.)
Maps are not inherited from Collection, and will be treated
separately.
|
boolean
add(Object) |
Ensures that the container holds the
argument. Returns false if it doesn’t add the argument. (This is an
“optional” method, described later in this
chapter.) |
|
boolean
|
Adds all the elements in the argument.
Returns true if any elements were added.
(“Optional.”) |
|
void
clear( ) |
Removes all the elements in the
container. (“Optional.”) |
|
boolean
|
true if the container holds the
argument. |
|
boolean
containsAll(Collection) |
true if the container holds all
the elements in the argument. |
|
boolean
isEmpty( ) |
true if the container has no
elements. |
|
Iterator
iterator( ) |
Returns an Iterator that you can
use to move through the elements in the container. |
|
boolean
|
If the argument is in the container, one
instance of that element is removed. Returns true if a removal occurred.
(“Optional.”) |
|
boolean
removeAll(Collection) |
Removes all the elements that are
contained in the argument. Returns true if any removals occurred.
(“Optional.”) |
|
boolean
retainAll(Collection) |
Retains only elements that are contained
in the argument (an “intersection” from set theory). Returns
true if any changes occurred. (“Optional.”) |
|
int size( ) |
Returns the number of elements in the
container. |
|
Object[]
toArray( ) |
Returns an array containing all the
elements in the container. |
|
Object[]
|
Returns an array containing all the
elements in the container, whose type is that of the array a rather than plain
Object (you must cast the array to the right type). |
Notice that there’s no
get( ) function for random-access element selection. That’s
because Collection also includes Set, which maintains its own
internal ordering (and thus makes random-access lookup meaningless). Thus, if
you want to examine all the elements of a Collection you must use an
iterator; that’s the only way to fetch things back.
The following example demonstrates all of
these methods. Again, these work with anything that inherits from
Collection, but an ArrayList is used as a kind of
“least-common denominator”:
//: c09:Collection1.java
// Things you can do with all Collections.
import java.util.*;
import com.bruceeckel.util.*;
public class Collection1 {
public static void main(String[] args) {
Collection c = new ArrayList();
Collections2.fill(c,
Collections2.countries, 10);
c.add("ten");
c.add("eleven");
System.out.println(c);
// Make an array from the List:
Object[] array = c.toArray();
// Make a String array from the List:
String[] str =
(String[])c.toArray(new String[1]);
// Find max and min elements; this means
// different things depending on the way
// the Comparable interface is implemented:
System.out.println("Collections.max(c) = " +
Collections.max(c));
System.out.println("Collections.min(c) = " +
Collections.min(c));
// Add a Collection to another Collection
Collection c2 = new ArrayList();
Collections2.fill(c2,
Collections2.countries, 10);
c.addAll(c2);
System.out.println(c);
c.remove(CountryCapitals.pairs[0][0]);
System.out.println(c);
c.remove(CountryCapitals.pairs[1][0]);
System.out.println(c);
// Remove all components that are in the
// argument collection:
c.removeAll(c2);
System.out.println(c);
c.addAll(c2);
System.out.println(c);
// Is an element in this Collection?
String val = CountryCapitals.pairs[3][0];
System.out.println(
"c.contains(" + val + ") = "
+ c.contains(val));
// Is a Collection in this Collection?
System.out.println(
"c.containsAll(c2) = "+ c.containsAll(c2));
Collection c3 = ((List)c).subList(3, 5);
// Keep all the elements that are in both
// c2 and c3 (an intersection of sets):
c2.retainAll(c3);
System.out.println(c);
// Throw away all the elements
// in c2 that also appear in c3:
c2.removeAll(c3);
System.out.println("c.isEmpty() = " +
c.isEmpty());
c = new ArrayList();
Collections2.fill(c,
Collections2.countries, 10);
System.out.println(c);
c.clear(); // Remove all elements
System.out.println("after c.clear():");
System.out.println(c);
}
} ///:~ArrayLists are created containing
different sets of data and upcast to Collection objects, so it’s
clear that nothing other than the Collection interface is being used.
main( ) uses simple exercises to show all of the methods in
Collection.
The following sections describe the
various implementations of List, Set, and Map and indicate
in each case (with an asterisk) which one should be your default choice.
You’ll notice that the legacy classes Vector, Stack, and
Hashtable are not included because in all cases there are
preferred classes within the Java 2
Containers.
The basic List is quite simple to
use, as you’ve seen so far with ArrayList. Although most of the
time you’ll just use add( ) to insert objects,
get( ) to get them out one at a time, and iterator( ) to
get an Iterator to the sequence, there’s also a set of other
methods that can be useful.
In addition, there are actually two types
of List: the basic ArrayList, which excels at randomly accessing
elements, and the much more powerful LinkedList (which is not designed
for fast random access, but has a much more general set of
methods).
|
List (interface) |
Order is the most important feature of a
List; it promises to maintain elements in a particular sequence.
List adds a number of methods to Collection that allow insertion
and removal of elements in the middle of a List. (This is recommended
only for a LinkedList.) A List will produce a ListIterator,
and using this you can traverse the List in both directions, as well as
insert and remove elements in the middle of the List. |
|
ArrayList* |
A List implemented with an array.
Allows rapid random access to elements, but is slow when inserting and removing
elements from the middle of a list. ListIterator should be used only for
back-and-forth traversal of an ArrayList, but not for inserting and
removing elements, which is expensive compared to
LinkedList. |
|
LinkedList |
Provides optimal sequential access, with
inexpensive insertions and deletions from the middle of the List.
Relatively slow for random access. (Use ArrayList instead.) Also has
addFirst( ), addLast( ), getFirst( ),
getLast( ), removeFirst( ), and
removeLast( ) (which are not defined in any interfaces or base
classes) to allow it to be used as a stack, a queue, and a
deque. |
The methods in the following example each
cover a different group of activities: things that every list can do
(basicTest( )), moving around with an Iterator
(iterMotion( )) versus changing things with an
Iterator (iterManipulation( )), seeing the effects of
List manipulation (testVisual( )), and operations available
only to LinkedLists.
//: c09:List1.java
// Things you can do with Lists.
import java.util.*;
import com.bruceeckel.util.*;
public class List1 {
public static List fill(List a) {
Collections2.countries.reset();
Collections2.fill(a,
Collections2.countries, 10);
return a;
}
static boolean b;
static Object o;
static int i;
static Iterator it;
static ListIterator lit;
public static void basicTest(List a) {
a.add(1, "x"); // Add at location 1
a.add("x"); // Add at end
// Add a collection:
a.addAll(fill(new ArrayList()));
// Add a collection starting at location 3:
a.addAll(3, fill(new ArrayList()));
b = a.contains("1"); // Is it in there?
// Is the entire collection in there?
b = a.containsAll(fill(new ArrayList()));
// Lists allow random access, which is cheap
// for ArrayList, expensive for LinkedList:
o = a.get(1); // Get object at location 1
i = a.indexOf("1"); // Tell index of object
b = a.isEmpty(); // Any elements inside?
it = a.iterator(); // Ordinary Iterator
lit = a.listIterator(); // ListIterator
lit = a.listIterator(3); // Start at loc 3
i = a.lastIndexOf("1"); // Last match
a.remove(1); // Remove location 1
a.remove("3"); // Remove this object
a.set(1, "y"); // Set location 1 to "y"
// Keep everything that's in the argument
// (the intersection of the two sets):
a.retainAll(fill(new ArrayList()));
// Remove everything that's in the argument:
a.removeAll(fill(new ArrayList()));
i = a.size(); // How big is it?
a.clear(); // Remove all elements
}
public static void iterMotion(List a) {
ListIterator it = a.listIterator();
b = it.hasNext();
b = it.hasPrevious();
o = it.next();
i = it.nextIndex();
o = it.previous();
i = it.previousIndex();
}
public static void iterManipulation(List a) {
ListIterator it = a.listIterator();
it.add("47");
// Must move to an element after add():
it.next();
// Remove the element that was just produced:
it.remove();
// Must move to an element after remove():
it.next();
// Change the element that was just produced:
it.set("47");
}
public static void testVisual(List a) {
System.out.println(a);
List b = new ArrayList();
fill(b);
System.out.print("b = ");
System.out.println(b);
a.addAll(b);
a.addAll(fill(new ArrayList()));
System.out.println(a);
// Insert, remove, and replace elements
// using a ListIterator:
ListIterator x = a.listIterator(a.size()/2);
x.add("one");
System.out.println(a);
System.out.println(x.next());
x.remove();
System.out.println(x.next());
x.set("47");
System.out.println(a);
// Traverse the list backwards:
x = a.listIterator(a.size());
while(x.hasPrevious())
System.out.print(x.previous() + " ");
System.out.println();
System.out.println("testVisual finished");
}
// There are some things that only
// LinkedLists can do:
public static void testLinkedList() {
LinkedList ll = new LinkedList();
fill(ll);
System.out.println(ll);
// Treat it like a stack, pushing:
ll.addFirst("one");
ll.addFirst("two");
System.out.println(ll);
// Like "peeking" at the top of a stack:
System.out.println(ll.getFirst());
// Like popping a stack:
System.out.println(ll.removeFirst());
System.out.println(ll.removeFirst());
// Treat it like a queue, pulling elements
// off the tail end:
System.out.println(ll.removeLast());
// With the above operations, it's a dequeue!
System.out.println(ll);
}
public static void main(String[] args) {
// Make and fill a new list each time:
basicTest(fill(new LinkedList()));
basicTest(fill(new ArrayList()));
iterMotion(fill(new LinkedList()));
iterMotion(fill(new ArrayList()));
iterManipulation(fill(new LinkedList()));
iterManipulation(fill(new ArrayList()));
testVisual(fill(new LinkedList()));
testLinkedList();
}
} ///:~In basicTest( ) and
iterMotion( ) the calls are simply made to show the proper syntax,
and while the return value is captured, it is not used. In some cases, the
return value isn’t captured since it isn’t typically used. You
should look up the full usage of each of these methods in the online
documentation from java.sun.com before you use
them.
A stack is
sometimes referred to as a “last-in, first-out”
(LIFO) container. That is, whatever you
“push” on the stack last is the first item you can “pop”
out. Like all of the other containers in Java, what you push and pop are
Objects, so you must cast what you pop, unless you’re just using
Object behavior.
The LinkedList has methods that
directly implement stack functionality, so you can also just use a
LinkedList rather than making a stack class. However, a stack class can
sometimes tell the story better:
//: c09:StackL.java
// Making a stack from a LinkedList.
import java.util.*;
import com.bruceeckel.util.*;
public class StackL {
private LinkedList list = new LinkedList();
public void push(Object v) {
list.addFirst(v);
}
public Object top() { return list.getFirst(); }
public Object pop() {
return list.removeFirst();
}
public static void main(String[] args) {
StackL stack = new StackL();
for(int i = 0; i < 10; i++)
stack.push(Collections2.countries.next());
System.out.println(stack.top());
System.out.println(stack.top());
System.out.println(stack.pop());
System.out.println(stack.pop());
System.out.println(stack.pop());
}
} ///:~If you want only stack behavior,
inheritance is inappropriate here because it would produce a class with all the
rest of the LinkedList methods (you’ll see later that this very
mistake was made by the Java 1.0 library designers with
Stack).
A queue is
a “first-in, first-out” (FIFO)
container. That is, you put things in at one end, and pull them out at the
other. So the order in which you put them in will be the same order that they
come out. LinkedList has methods to support queue
behavior, so these can be used in a Queue class:
//: c09:Queue.java
// Making a queue from a LinkedList.
import java.util.*;
public class Queue {
private LinkedList list = new LinkedList();
public void put(Object v) { list.addFirst(v); }
public Object get() {
return list.removeLast();
}
public boolean isEmpty() {
return list.isEmpty();
}
public static void main(String[] args) {
Queue queue = new Queue();
for(int i = 0; i < 10; i++)
queue.put(Integer.toString(i));
while(!queue.isEmpty())
System.out.println(queue.get());
}
} ///:~You can also easily create a deque
(double-ended queue) from a LinkedList. This is like a queue, but you can
add and remove elements from either
end.
Set has exactly the same interface
as Collection, so there isn’t any extra functionality like there is
with the two different Lists. Instead, the Set is exactly a
Collection, it just has different behavior. (This is the ideal use of
inheritance and polymorphism: to express different behavior.) A Set
refuses to hold more than one instance of each object value (what constitutes
the “value” of an object is more complex, as you shall see).
|
Set (interface) |
Each element that you add to the
Set must be unique; otherwise the Set doesn’t add the
duplicate element. Objects added to a Set must define
equals( ) to establish object uniqueness. Set has exactly the
same interface as Collection. The Set interface does not guarantee
it will maintain its elements in any particular order. |
|
HashSet* |
For Sets where fast lookup time is
important. Objects must also define
hashCode( ). |
|
TreeSet |
An ordered Set backed by a tree.
This way, you can extract an ordered sequence from a
Set. |
The following example does not
show everything you can do with a Set, since the interface is the same as
Collection, and so was exercised in the previous example. Instead, this
demonstrates the behavior that makes a Set unique:
//: c09:Set1.java
// Things you can do with Sets.
import java.util.*;
import com.bruceeckel.util.*;
public class Set1 {
static Collections2.StringGenerator gen =
Collections2.countries;
public static void testVisual(Set a) {
Collections2.fill(a, gen.reset(), 10);
Collections2.fill(a, gen.reset(), 10);
Collections2.fill(a, gen.reset(), 10);
System.out.println(a); // No duplicates!
// Add another set to this one:
a.addAll(a);
a.add("one");
a.add("one");
a.add("one");
System.out.println(a);
// Look something up:
System.out.println("a.contains(\"one\"): " +
a.contains("one"));
}
public static void main(String[] args) {
System.out.println("HashSet");
testVisual(new HashSet());
System.out.println("TreeSet");
testVisual(new TreeSet());
}
} ///:~Duplicate values are added to the
Set, but when it is printed you’ll see the Set has accepted
only one instance of each value.
When you run this program you’ll
notice that the order maintained by the HashSet is different from
TreeSet, since each has a different way of storing elements so they can
be located later. (TreeSet keeps them sorted, while HashSet uses a
hashing function, which is designed specifically for rapid lookups.) When
creating your own types, be aware that a Set needs a way to maintain a
storage order, which means you must implement the Comparable interface
and define the compareTo( ) method. Here’s an
example:
//: c09:Set2.java
// Putting your own type in a Set.
import java.util.*;
class MyType implements Comparable {
private int i;
public MyType(int n) { i = n; }
public boolean equals(Object o) {
return
(o instanceof MyType)
&& (i == ((MyType)o).i);
}
public int hashCode() { return i; }
public String toString() { return i + " "; }
public int compareTo(Object o) {
int i2 = ((MyType)o).i;
return (i2 < i ? -1 : (i2 == i ? 0 : 1));
}
}
public class Set2 {
public static Set fill(Set a, int size) {
for(int i = 0; i < size; i++)
a.add(new MyType(i));
return a;
}
public static void test(Set a) {
fill(a, 10);
fill(a, 10); // Try to add duplicates
fill(a, 10);
a.addAll(fill(new TreeSet(), 10));
System.out.println(a);
}
public static void main(String[] args) {
test(new HashSet());
test(new TreeSet());
}
} ///:~The
form for the definitions for equals( ) and
hashCode( ) will be described later in this chapter. You must define
an equals( ) in both cases, but the hashCode( ) is
absolutely necessary only if the class will be placed in a HashSet (which
is likely, since that should generally be your first choice as a Set
implementation). However, as a programming style you should always override
hashCode( ) when you override equals( ). This process
will be fully detailed later in this chapter.
In the compareTo( ), note
that I did not use the “simple and obvious” form return
i-i2. Although this is a common programming error, it would only work
properly if i and i2 were “unsigned” ints (if
Java had an “unsigned” keyword, which it does not). It breaks
for Java’s signed int, which is not big enough to represent the
difference of two signed ints. If i is a large positive integer
and j is a large negative integer, i-j will overflow and return a
negative value, which will not work.
If you have a SortedSet (of which
TreeSet is the only one available), the elements are guaranteed to be in
sorted order which allows additional functionality to be provided with these
methods in the SortedSet interface:
Comparator comparator(): Produces
the Comparator used for this Set, or null for natural
ordering.
Object first(): Produces the
lowest element.
Object last(): Produces the
highest element.
SortedSet subSet(fromElement,
toElement): Produces a view of this Set with elements from
fromElement, inclusive, to toElement, exclusive.
SortedSet headSet(toElement):
Produces a view of this Set with elements less than toElement.
SortedSet tailSet(fromElement):
Produces a view of this Set with elements greater than or equal to
fromElement.
An ArrayList allows you to select
from a sequence of objects using a number, so in a sense it associates numbers
to objects. But what if you’d like to select from a sequence of objects
using some other criterion? A stack is an example: its selection criterion is
“the last thing pushed on the stack.” A powerful twist on this idea
of “selecting from a sequence” is alternately termed a
map, a dictionary,
or an associative array.
Conceptually, it seems like an ArrayList, but instead of looking up
objects using a number, you look them up using another object! This is
often a key process in a program.
The concept shows up in Java as the
Map interface. The put(Object key, Object value) method adds a
value (the thing you want), and associates it with a key (the thing you look it
up with). get(Object key) produces the value given the corresponding key.
You can also test a Map to see if it contains a key or a value with
containsKey( ) and containsValue( ).
The standard Java library contains two
different types of Maps: HashMap and TreeMap. Both have the
same interface (since they both implement Map), but they differ in one
distinct way: efficiency. If you look at what must be done for a
get( ), it seems pretty slow to search through (for example) an
ArrayList for the key. This is where HashMap speeds things up.
Instead of a slow search for the key, it uses a special value called a
hash code. The hash code is a way to take
some information in the object in question and turn it into a “relatively
unique” int for that object. All Java objects can produce a hash
code, and hashCode( ) is a method in the root
class Object. A HashMap takes the
hashCode( ) of the object and uses it to quickly hunt for the key.
This results in a dramatic performance
improvement[51].
|
Map (interface) |
Maintains key-value associations (pairs),
so you can look up a value using a key. |
|
HashMap* |
Implementation based on a hash table.
(Use this instead of Hashtable.) Provides constant-time performance for
inserting and locating pairs. Performance can be adjusted via constructors that
allow you to set the capacity and load factor of the hash
table. |
|
TreeMap |
Implementation based on a red-black tree.
When you view the keys or the pairs, they will be in sorted order (determined by
Comparable or Comparator, discussed later). The point of a
TreeMap is that you get the results in sorted order. TreeMap is
the only Map with the subMap( ) method, which allows you to
return a portion of the tree. |
Sometimes you’ll also need to know
the details of how hashing works, so we’ll look at that a little
later.
The following example uses the
Collections2.fill( ) method and the test data sets that were
previously defined:
//: c09:Map1.java
// Things you can do with Maps.
import java.util.*;
import com.bruceeckel.util.*;
public class Map1 {
static Collections2.StringPairGenerator geo =
Collections2.geography;
static Collections2.RandStringPairGenerator
rsp = Collections2.rsp;
// Producing a Set of the keys:
public static void printKeys(Map m) {
System.out.print("Size = " + m.size() +", ");
System.out.print("Keys: ");
System.out.println(m.keySet());
}
// Producing a Collection of the values:
public static void printValues(Map m) {
System.out.print("Values: ");
System.out.println(m.values());
}
public static void test(Map m) {
Collections2.fill(m, geo, 25);
// Map has 'Set' behavior for keys:
Collections2.fill(m, geo.reset(), 25);
printKeys(m);
printValues(m);
System.out.println(m);
String key = CountryCapitals.pairs[4][0];
String value = CountryCapitals.pairs[4][1];
System.out.println("m.containsKey(\"" + key +
"\"): " + m.containsKey(key));
System.out.println("m.get(\"" + key + "\"): "
+ m.get(key));
System.out.println("m.containsValue(\""
+ value + "\"): " +
m.containsValue(value));
Map m2 = new TreeMap();
Collections2.fill(m2, rsp, 25);
m.putAll(m2);
printKeys(m);
key = m.keySet().iterator().next().toString();
System.out.println("First key in map: "+key);
m.remove(key);
printKeys(m);
m.clear();
System.out.println("m.isEmpty(): "
+ m.isEmpty());
Collections2.fill(m, geo.reset(), 25);
// Operations on the Set change the Map:
m.keySet().removeAll(m.keySet());
System.out.println("m.isEmpty(): "
+ m.isEmpty());
}
public static void main(String[] args) {
System.out.println("Testing HashMap");
test(new HashMap());
System.out.println("Testing TreeMap");
test(new TreeMap());
}
} ///:~The printKeys( ) and
printValues( ) methods are not only useful utilities, they also
demonstrate how to produce Collection views of a Map. The
keySet( ) method produces a Set backed by the keys in the
Map. Similar treatment is given to values( ), which produces
a Collection containing all the values in the Map. (Note that keys
must be unique, while values may contain duplicates.) Since these
Collections are backed by the Map, any changes in a
Collection will be reflected in the associated
Map.
The rest of the program provides simple
examples of each Map operation, and tests each type of
Map.
As an example of the use of a
HashMap, consider a program to check the randomness of Java’s
Math.random( ) method.
Ideally, it would produce a perfect distribution of random numbers, but to test
this you need to generate a bunch of random numbers and count the ones that fall
in the various ranges. A HashMap is perfect for this, since it associates
objects with objects (in this case, the value object contains the number
produced by Math.random( ) along with the number of times that
number appears):
//: c09:Statistics.java
// Simple demonstration of HashMap.
import java.util.*;
class Counter {
int i = 1;
public String toString() {
return Integer.toString(i);
}
}
class Statistics {
public static void main(String[] args) {
HashMap hm = new HashMap();
for(int i = 0; i < 10000; i++) {
// Produce a number between 0 and 20:
Integer r =
new Integer((int)(Math.random() * 20));
if(hm.containsKey(r))
((Counter)hm.get(r)).i++;
else
hm.put(r, new Counter());
}
System.out.println(hm);
}
} ///:~In main( ), each time a
random number is generated it is wrapped inside an Integer object so that
reference can be used with the HashMap. (You can’t use a primitive
with a container, only an object reference.) The containsKey( )
method checks to see if this key is already in the container. (That is, has the
number been found already?) If so, the get( )
method produces the associated value for the key, which in this case is a
Counter object. The value i inside the counter is incremented to
indicate that one more of this particular random number has been
found.
If the key has not been found yet, the
method put( ) will place a new key-value pair
into the HashMap. Since Counter automatically initializes its
variable i to one when it’s created, it indicates the first
occurrence of this particular random number.
To display the HashMap, it is
simply printed. The HashMap toString( ) method moves through
all the key-value pairs and calls the toString( ) for each one. The
Integer.toString( ) is predefined, and you can see the
toString( ) for Counter. The output from one run (with some
line breaks added) is:
{19=526, 18=533, 17=460, 16=513, 15=521, 14=495,
13=512, 12=483, 11=488, 10=487, 9=514, 8=523,
7=497, 6=487, 5=480, 4=489, 3=509, 2=503, 1=475,
0=505}You might wonder at the necessity of the
class Counter, which seems like it doesn’t even have the
functionality of the wrapper class Integer. Why not use int or
Integer? Well, you can’t use an int because all of the
containers can hold only Object references. After seeing containers the
wrapper classes might begin to make a little more sense to you, since you
can’t put any of the primitive types in containers. However, the only
thing you can do with the Java wrappers is to
initialize them to a particular value and read that value. That is,
there’s no way to change a value once a wrapper object has been created.
This makes the Integer wrapper immediately useless to solve our problem,
so we’re forced to create a new class that does satisfy the
need.
If you have a SortedMap (of which
TreeMap is the only one available), the keys are guaranteed to be in
sorted order which allows additional functionality to be provided with these
methods in the SortedMap interface:
Comparator comparator(): Produces
the comparator used for this Map, or null for natural ordering.
Object firstKey(): Produces the
lowest key.
Object lastKey(): Produces the
highest key.
SortedMap subMap(fromKey, toKey):
Produces a view of this Map with keys from fromKey, inclusive, to
toKey, exclusive.
SortedMap headMap(toKey): Produces
a view of this Map with keys less than toKey.
In the previous example, a standard
library class (Integer) was used as a key for the HashMap. It
worked fine as a key, because it has all the necessary wiring to make it work
correctly as a key. But a common pitfall occurs with HashMaps when you
create your own classes to be used as keys. For example, consider a weather
predicting system that matches Groundhog objects to Prediction
objects. It seems fairly straightforward—you create the two classes, and
use Groundhog as the key and Prediction as the
value:
//: c09:SpringDetector.java
// Looks plausible, but doesn't work.
import java.util.*;
class Groundhog {
int ghNumber;
Groundhog(int n) { ghNumber = n; }
}
class Prediction {
boolean shadow = Math.random() > 0.5;
public String toString() {
if(shadow)
return "Six more weeks of Winter!";
else
return "Early Spring!";
}
}
public class SpringDetector {
public static void main(String[] args) {
HashMap hm = new HashMap();
for(int i = 0; i < 10; i++)
hm.put(new Groundhog(i), new Prediction());
System.out.println("hm = " + hm + "\n");
System.out.println(
"Looking up prediction for Groundhog #3:");
Groundhog gh = new Groundhog(3);
if(hm.containsKey(gh))
System.out.println((Prediction)hm.get(gh));
else
System.out.println("Key not found: " + gh);
}
} ///:~Each Groundhog is given an
identity number, so you can look up a Prediction in the HashMap by
saying, “Give me the Prediction associated with Groundhog
number 3.” The Prediction class contains a boolean that is
initialized using Math.random( ), and a toString( ) that
interprets the result for you. In main( ), a HashMap is
filled with Groundhogs and their associated Predictions. The
HashMap is printed so you can see that it has been filled. Then a
Groundhog with an identity number of 3 is used as a key to look up the
prediction for Groundhog #3 (which you can see must be in the
Map).
It seems simple enough, but it
doesn’t work. The problem is that Groundhog is inherited from the
common root class Object (which is what happens if you don’t
specify a base class, thus all classes are ultimately inherited from
Object). It is Object’s hashCode( ) method that
is used to generate the hash code for each object, and by default it just uses
the address of its object. Thus, the first instance of Groundhog(3) does
not produce a hash code equal to the hash code for the second instance of
Groundhog(3) that we tried to use as a lookup.
You might think that all you need to do
is write an appropriate override for
hashCode( ). But it still won’t work
until you’ve done one more thing: override the
equals( ) that is also part of Object.
This method is used by the HashMap when trying to determine if your key
is equal to any of the keys in the table. Again, the default
Object.equals( ) simply compares object addresses, so one
Groundhog(3) is not equal to another
Groundhog(3).
Thus, to use your own classes as keys in
a HashMap, you must override both hashCode( ) and
equals( ), as shown in the following solution to the problem
above:
//: c09:SpringDetector2.java
// A class that's used as a key in a HashMap
// must override hashCode() and equals().
import java.util.*;
class Groundhog2 {
int ghNumber;
Groundhog2(int n) { ghNumber = n; }
public int hashCode() { return ghNumber; }
public boolean equals(Object o) {
return (o instanceof Groundhog2)
&& (ghNumber == ((Groundhog2)o).ghNumber);
}
}
public class SpringDetector2 {
public static void main(String[] args) {
HashMap hm = new HashMap();
for(int i = 0; i < 10; i++)
hm.put(new Groundhog2(i),new Prediction());
System.out.println("hm = " + hm + "\n");
System.out.println(
"Looking up prediction for groundhog #3:");
Groundhog2 gh = new Groundhog2(3);
if(hm.containsKey(gh))
System.out.println((Prediction)hm.get(gh));
}
} ///:~Note that this uses the Prediction
class from the previous example, so SpringDetector.java must be compiled
first or you’ll get a compile-time error when you try to compile
SpringDetector2.java.
Groundhog2.hashCode( )
returns the groundhog number as an identifier. In this example, the programmer
is responsible for ensuring that no two groundhogs exist with the same ID
number. The hashCode( ) is not required to return a unique
identifier (something you’ll understand better later in this chapter), but
the equals( ) method must be able to strictly determine whether two
objects are equivalent.
Even though it appears that the
equals( ) method is only checking to see whether the argument is an
instance of Groundhog2 (using the instanceof keyword, which is
fully explained in Chapter 12), the instanceof actually quietly does a
second sanity check, to see if the object is null, since
instanceof produces false if the left-hand argument is
null. Assuming it’s the correct type and not null, the
comparison is based on the actual ghNumbers. This time, when you run the
program, you’ll see it produces the correct output.
When creating your own class to use in a
HashSet, you must pay attention to the same issues as when it is used as
a key in a HashMap.
The above example is only a start toward
solving the problem correctly. It shows that if you do not override
hashCode( ) and
equals( ) for your key, the hashed data
structure (HashSet or HashMap) will not be able to deal with your
key properly. However, to get a good solution for the problem you need to
understand what’s going on inside the hashed data
structure.
First, consider the motivation behind
hashing: you want to look up an object using another
object. But you can accomplish this with a TreeSet or TreeMap,
too. It’s also possible to implement your own Map. To do so, the
Map.entrySet( ) method must be supplied to produce a set of
Map.Entry objects. MPair will be defined as the new type of
Map.Entry. In order for it to be placed in a
TreeSet it must implement equals( ) and be
Comparable:
//: c09:MPair.java
// A Map implemented with ArrayLists.
import java.util.*;
public class MPair
implements Map.Entry, Comparable {
Object key, value;
MPair(Object k, Object v) {
key = k;
value = v;
}
public Object getKey() { return key; }
public Object getValue() { return value; }
public Object setValue(Object v){
Object result = value;
value = v;
return result;
}
public boolean equals(Object o) {
return key.equals(((MPair)o).key);
}
public int compareTo(Object rv) {
return ((Comparable)key).compareTo(
((MPair)rv).key);
}
} ///:~Notice that the comparisons are only interested in the keys, so duplicate values are perfectly acceptable.
The
following example implements a Map using a pair of
ArrayLists:
//: c09:SlowMap.java
// A Map implemented with ArrayLists.
import java.util.*;
import com.bruceeckel.util.*;
public class SlowMap extends AbstractMap {
private ArrayList
keys = new ArrayList(),
values = new ArrayList();
public Object put(Object key, Object value) {
Object result = get(key);
if(!keys.contains(key)) {
keys.add(key);
values.add(value);
} else
values.set(keys.indexOf(key), value);
return result;
}
public Object get(Object key) {
if(!keys.contains(key))
return null;
return values.get(keys.indexOf(key));
}
public Set entrySet() {
Set entries = new HashSet();
Iterator
ki = keys.iterator(),
vi = values.iterator();
while(ki.hasNext())
entries.add(new MPair(ki.next(), vi.next()));
return entries;
}
public static void main(String[] args) {
SlowMap m = new SlowMap();
Collections2.fill(m,
Collections2.geography, 25);
System.out.println(m);
}
} ///:~The put( ) method simply
places the keys and values in corresponding ArrayLists. In
main( ), a SlowMap is loaded and then printed to show that it
works.
This shows that it’s not that hard
to produce a new type of Map. But as the name suggests, a SlowMap
isn’t very fast, so you probably wouldn’t use it if you had an
alternative available. The problem is in the lookup of the key: there is no
order so a simple linear search is used, which is the slowest way to look
something up.
The whole point of hashing is speed:
hashing allows the lookup to happen quickly. Since the bottleneck is in the
speed of the key lookup, one of the solutions to the problem could be by keeping
the keys sorted and then using Collections.binarySearch( ) to
perform the lookup (an exercise at the end of this chapter will walk you through
this process).
Hashing goes further by saying that all
you want to do is to store the key somewhere so that it can be quickly
found. As you’ve seen in this chapter, the fastest structure in which to
store a group of elements is an array, so that will used for representing the
key information (note carefully that I said “key information,” and
not the key itself). Also seen in this chapter was the fact that an array, once
allocated, cannot be resized, so we have a problem: we want to be able to store
any number of values in the Map, but if the number of keys is fixed by
the array size, how can this be?
The answer is that the array will not
hold the keys. From the key object, a number will be derived that will index
into the array. This number is the hash code,
produced by the hashCode( ) method (in computer science parlance,
this is the hash function) defined in
Object and presumably overridden by your class. To solve the problem of
the fixed-size array, more than one key may produce the same index. That is,
there may be collisions. Because of this, it
doesn’t matter how big the array is because each key object will land
somewhere in that array.
So the process of looking up a value
starts by computing the hash code and using it to index into the array. If you
could guarantee that there were no collisions (which could be possible if you
have a fixed number of values) then you’d have a
perfect hashing function,
but that’s a special case. In all other cases, collisions are handled by
external chaining: the array points not directly
to a value, but instead to a list of values. These values are searched in a
linear fashion using the equals( ) method. Of course, this aspect of
the search is much slower, but if the hash function is good there will only be a
few values in each slot, at the most. So instead of searching through the entire
list, you quickly jump to a slot where you have to compare a few entries to find
the value. This is much faster, which is why the HashMap is so
quick.
Knowing the basics of hashing, it’s
possible to implement a simple hashed Map:
//: c09:SimpleHashMap.java
// A demonstration hashed Map.
import java.util.*;
import com.bruceeckel.util.*;
public class SimpleHashMap extends AbstractMap {
// Choose a prime number for the hash table
// size, to achieve a uniform distribution:
private final static int SZ = 997;
private LinkedList[] bucket= new LinkedList[SZ];
public Object put(Object key, Object value) {
Object result = null;
int index = key.hashCode() % SZ;
if(index < 0) index = -index;
if(bucket[index] == null)
bucket[index] = new LinkedList();
LinkedList pairs = bucket[index];
MPair pair = new MPair(key, value);
ListIterator it = pairs.listIterator();
boolean found = false;
while(it.hasNext()) {
Object iPair = it.next();
if(iPair.equals(pair)) {
result = ((MPair)iPair).getValue();
it.set(pair); // Replace old with new
found = true;
break;
}
}
if(!found)
bucket[index].add(pair);
return result;
}
public Object get(Object key) {
int index = key.hashCode() % SZ;
if(index < 0) index = -index;
if(bucket[index] == null) return null;
LinkedList pairs = bucket[index];
MPair match = new MPair(key, null);
ListIterator it = pairs.listIterator();
while(it.hasNext()) {
Object iPair = it.next();
if(iPair.equals(match))
return ((MPair)iPair).getValue();
}
return null;
}
public Set entrySet() {
Set entries = new HashSet();
for(int i = 0; i < bucket.length; i++) {
if(bucket[i] == null) continue;
Iterator it = bucket[i].iterator();
while(it.hasNext())
entries.add(it.next());
}
return entries;
}
public static void main(String[] args) {
SimpleHashMap m = new SimpleHashMap();
Collections2.fill(m,
Collections2.geography, 25);
System.out.println(m);
}
} ///:~Because the “slots” in a hash
table are often referred to as buckets, the array that represents the
actual table is called bucket. To promote even distribution, the number
of buckets is typically a prime number. Notice that it is an array of
LinkedList, which automatically provides for collisions—each new
item is simply added to the end of the list.
The return value of put( ) is
null or, if the key was already in the list, the old value associated
with that key. The return value is result, which is initialized to
null, but if a key is discovered in the list then result is
assigned to that key.
For both put( ) and
get( ), the first thing that happens is that the
hashCode( ) is called for the key, and the result is forced to a
positive number. Then it is forced to fit into the bucket array using the
modulus operator and the size of the array. If that location is null, it
means there are no elements that hash to that location, so a new
LinkedList is created to hold the object that just did. However, the
normal process is to look through the list to see if there are duplicates, and
if there are, the old value is put into result and the new value replaces
the old. The found flag keeps track of whether an old key-value pair was
found and, if not, the new pair is appended to the end of the
list.
In get( ), you’ll see
very similar code as that contained in put( ), but simpler. The
index is calculated into the bucket array, and if a LinkedList
exists it is searched for a match.
entrySet( ) must find and
traverse all the lists, adding them to the result Set. Once this method
has been created, the Map can be tested by filling it with values and
then printing them.
To understand the issues, some
terminology is necessary:
Initial
capacity: The number of buckets when the table is created.
HashMap and HashSet: have constructors that allow you to specify
the initial capacity.
Load
factor: size/capacity. A load factor of 0 is an empty table, 0.5
is a half-full table, etc. A lightly-loaded table will have few collisions and
so is optimal for insertions and lookups (but will slow down the process of
traversing with an iterator). HashMap and HashSet have
constructors that allow you to specify the load factor, which means that when
this load factor is reached the container will automatically increase the
capacity (the number of buckets) by roughly doubling it, and will redistribute
the existing objects into the new set of buckets (this is called
rehashing).
The default load factor used by
HashMap is 0.75 (it doesn’t rehash until the table is ¾ full).
This seems to be a good trade-off between time and space costs. A higher load
factor decreases the space required by the table but increases the lookup cost,
which is important because lookup is what you do most of the time (including
both get( ) and put( )).
If you know that you’ll be storing
many entries in a HashMap, creating it with an appropriately large
initial capacity will prevent the overhead of automatic
rehashing.
Now that you understand what’s
involved in the function of the HashMap, the issues involved in writing a
hashCode( ) will make more
sense.
First of all, you don’t have
control of the creation of the actual value that’s used to index into the
array of buckets. That is dependent on the capacity of the particular
HashMap object, and that capacity changes depending on how full the
container is, and what the load factor is. The value produced by your
hashCode( ) will be further processed in order to create the bucket
index (in SimpleHashMap the calculation is just a modulo by the size of
the bucket array).
The most important factor in creating a
hashCode( ) is that, regardless of when hashCode( ) is
called, it produces the same value for a particular object every time it is
called. If you end up with an object that produces one hashCode( )
value when it is put( ) into a HashMap, and another
during a get( ), you won’t be able to retrieve the objects. So
if your hashCode( ) depends on mutable data in the object the user
must be made aware that changing the data will effectively produce a different
key by generating a different hashCode( ).
In addition, you will probably not
want to generate a hashCode( ) that is based on unique object
information—in particular, the value of this makes a bad
hashCode( ) because then you can’t generate a new identical
key to the one used to put( ) the original key-value pair. This was
the problem that occurred in SpringDetector.java because the default
implementation of hashCode( ) does use the object address. So
you’ll want to use information in the object that identifies the object in
a meaningful way.
One example is found in the String
class. Strings have the special characteristic that if a program has
several String objects that contain identical character sequences, then
those String objects all map to the same memory (the mechanism for this
is described in Appendix A). So it makes sense that the hashCode( )
produced by two separate instances of new String(“hello”)
should be identical. You can see it by running this program:
//: c09:StringHashCode.java
public class StringHashCode {
public static void main(String[] args) {
System.out.println("Hello".hashCode());
System.out.println("Hello".hashCode());
}
} ///:~For this to work, the
hashCode( ) for String must be based on the contents of the
String.
So for a hashCode( ) to be
effective, it must be fast and it must be meaningful: that is, it must generate
a value based on the contents of the object. Remember that this value
doesn’t have to be unique—you should lean toward speed rather than
uniqueness—but between hashCode( ) and equals( )
the identity of the object must be completely resolved.
Because the hashCode( ) is
further processed before the bucket index is produced, the range of values is
not important; it just needs to generate an int.
There’s one other factor: a good
hashCode( ) should result in an even distribution of values. If the
values tend to cluster, then the HashMap or HashSet will be more
heavily loaded in some areas and will not be as fast as it could be with an
evenly distributed hashing function.
Here’s an example that follows
these guidelines:
//: c09:CountedString.java
// Creating a good hashCode().
import java.util.*;
public class CountedString {
private String s;
private int id = 0;
private static ArrayList created =
new ArrayList();
public CountedString(String str) {
s = str;
created.add(s);
Iterator it = created.iterator();
// Id is the total number of instances
// of this string in use by CountedString:
while(it.hasNext())
if(it.next().equals(s))
id++;
}
public String toString() {
return "String: " + s + " id: " + id +
" hashCode(): " + hashCode() + "\n";
}
public int hashCode() {
return s.hashCode() * id;
}
public boolean equals(Object o) {
return (o instanceof CountedString)
&& s.equals(((CountedString)o).s)
&& id == ((CountedString)o).id;
}
public static void main(String[] args) {
HashMap m = new HashMap();
CountedString[] cs = new CountedString[10];
for(int i = 0; i < cs.length; i++)
m.put(new Integer(i),
new CountedString("hi"));
System.out.println(m);
}
} ///:~CountedString includes a
String and an id that represents the number of
CountedString objects that contain an identical String. The
counting is accomplished in the constructor by iterating through the static
ArrayList where all the Strings are stored.
Both hashCode( ) and
equals( ) produce results based on both fields; if they were just
based on the String alone or the id alone there would be duplicate
matches for distinct values.
Note how simple the
hashCode( ) is: String’s hashCode( ) is
multiplied by the id. Smaller is generally better (and faster) for
hashCode( ).
In main( ), a bunch of
CountedString objects are created, using the same String to show
that the duplicates create unique values because of the count
id.
The java.lang.ref library contains
a set of classes that allow greater flexibility in garbage collection, which are
especially useful when you have large objects that may cause memory exhaustion.
There are three classes inherited from the abstract class
Reference:
SoftReference,
WeakReference, and
PhantomReference. Each of these provides a different
level of indirection for the garbage collector, if the object in question is
only reachable through one of these Reference objects.
If an object is
reachable it means that
somewhere in your program the object can be found. This could mean that you have
an ordinary reference on the stack that goes right to the object, but you might
also have a reference to an object that has a reference to the object in
question; there could be many intermediate links. If an object is reachable, the
garbage collector cannot release it because it’s still in use by your
program. If an object isn’t reachable, there’s no way for your
program to use it so it’s safe to garbage-collect that
object.
You use Reference objects when you
want to continue to hold onto a reference to that object—you want to be
able to reach that object—but you also want to allow the garbage collector
to release that object. Thus, you have a way to go on using the object, but if
memory exhaustion is imminent you allow that object to
be released.
You accomplish this by using a
Reference object as an intermediary between you and the ordinary
reference, and there must be no ordinary references to the object (ones
that are not wrapped inside Reference objects). If the garbage collector
discovers that an object is reachable through an ordinary reference, it will not
release that object.
In the order SoftReference,
WeakReference, and PhantomReference, each one is “weaker”
than the last, and corresponds to a different level of reachability. Soft
references are for implementing memory-sensitive caches. Weak references are for
implementing “canonicalizing mappings”—where instances of
objects can be simultaneously used in multiple places in a program, to save
storage—that do not prevent their keys (or values) from being reclaimed.
Phantom references are for scheduling pre-mortem cleanup actions in a more
flexible way than is possible with the Java finalization
mechanism.
With SoftReferences and
WeakReferences, you have a choice about whether to place them on a
ReferenceQueue (the device used for premortem cleanup actions), but a
PhantomReference can only be built on a ReferenceQueue.
Here’s a simple demonstration:
//: c09:References.java
// Demonstrates Reference objects
import java.lang.ref.*;
class VeryBig {
static final int SZ = 10000;
double[] d = new double[SZ];
String ident;
public VeryBig(String id) { ident = id; }
public String toString() { return ident; }
public void finalize() {
System.out.println("Finalizing " + ident);
}
}
public class References {
static ReferenceQueue rq= new ReferenceQueue();
public static void checkQueue() {
Object inq = rq.poll();
if(inq != null)
System.out.println("In queue: " +
(VeryBig)((Reference)inq).get());
}
public static void main(String[] args) {
int size = 10;
// Or, choose size via the command line:
if(args.length > 0)
size = Integer.parseInt(args[0]);
SoftReference[] sa =
new SoftReference[size];
for(int i = 0; i < sa.length; i++) {
sa[i] = new SoftReference(
new VeryBig("Soft " + i), rq);
System.out.println("Just created: " +
(VeryBig)sa[i].get());
checkQueue();
}
WeakReference[] wa =
new WeakReference[size];
for(int i = 0; i < wa.length; i++) {
wa[i] = new WeakReference(
new VeryBig("Weak " + i), rq);
System.out.println("Just created: " +
(VeryBig)wa[i].get());
checkQueue();
}
SoftReference s = new SoftReference(
new VeryBig("Soft"));
WeakReference w = new WeakReference(
new VeryBig("Weak"));
System.gc();
PhantomReference[] pa =
new PhantomReference[size];
for(int i = 0; i < pa.length; i++) {
pa[i] = new PhantomReference(
new VeryBig("Phantom " + i), rq);
System.out.println("Just created: " +
(VeryBig)pa[i].get());
checkQueue();
}
}
} ///:~When you run this program (you’ll
want to pipe the output through a “more” utility so that you can
view the output in pages), you’ll see that the objects are
garbage-collected, even though you still have access to them through the
Reference object (to get the actual object reference, you use
get( )). You’ll also see that the ReferenceQueue always
produces a Reference containing a null object. To make use of
this, you can inherit from the particular Reference class you’re
interested in and add more useful methods to the new type of
Reference.
The containers library has a special
Map to hold weak references: the
WeakHashMap. This class is designed to make the
creation of canonicalized mappings easier. In such a mapping, you are saving
storage by making only one instance of a particular value. When the program
needs that value, it looks up the existing object in the mapping and uses that
(rather than creating one from scratch). The mapping may make the values as part
of its initialization, but it’s more likely that the values are made on
demand.
Since this is a storage-saving technique,
it’s very convenient that the WeakHashMap allows the garbage
collector to automatically clean up the keys and values. You don’t have to
do anything special to the keys and values you want to place in the
WeakHashMap; these are automatically wrapped in WeakReferences by
the map. The trigger to allow cleanup is if the key is no longer in use, as
demonstrated here:
//: c09:CanonicalMapping.java
// Demonstrates WeakHashMap.
import java.util.*;
import java.lang.ref.*;
class Key {
String ident;
public Key(String id) { ident = id; }
public String toString() { return ident; }
public int hashCode() {
return ident.hashCode();
}
public boolean equals(Object r) {
return (r instanceof Key)
&& ident.equals(((Key)r).ident);
}
public void finalize() {
System.out.println("Finalizing Key "+ ident);
}
}
class Value {
String ident;
public Value(String id) { ident = id; }
public String toString() { return ident; }
public void finalize() {
System.out.println("Finalizing Value "+ident);
}
}
public class CanonicalMapping {
public static void main(String[] args) {
int size = 1000;
// Or, choose size via the command line:
if(args.length > 0)
size = Integer.parseInt(args[0]);
Key[] keys = new Key[size];
WeakHashMap whm = new WeakHashMap();
for(int i = 0; i < size; i++) {
Key k = new Key(Integer.toString(i));
Value v = new Value(Integer.toString(i));
if(i % 3 == 0)
keys[i] = k; // Save as "real" references
whm.put(k, v);
}
System.gc();
}
} ///:~The Key class must have a
hashCode( ) and an equals( ) since it is being used as a
key in a hashed data structure, as described previously in this
chapter.
When you run the program you’ll see
that the garbage collector will skip every third key, because an ordinary
reference to that key has also been placed in the keys array and thus
those objects cannot be
garbage-collected.
We can now demonstrate the true power of
the Iterator: the ability to separate the
operation of traversing a sequence from the underlying structure of that
sequence. In the following example, the class PrintData uses an
Iterator to move through a sequence and call the
toString( ) method for every object. Two
different types of containers are created—an
ArrayList and a
HashMap—and they are each filled with,
respectively, Mouse and Hamster objects. (These classes are
defined earlier in this chapter.) Because an Iterator hides the structure
of the underlying container, PrintData doesn’t know or care what
kind of container the Iterator comes from:
//: c09:Iterators2.java
// Revisiting Iterators.
import java.util.*;
class PrintData {
static void print(Iterator e) {
while(e.hasNext())
System.out.println(e.next());
}
}
class Iterators2 {
public static void main(String[] args) {
ArrayList v = new ArrayList();
for(int i = 0; i < 5; i++)
v.add(new Mouse(i));
HashMap m = new HashMap();
for(int i = 0; i < 5; i++)
m.put(new Integer(i), new Hamster(i));
System.out.println("ArrayList");
PrintData.print(v.iterator());
System.out.println("HashMap");
PrintData.print(m.entrySet().iterator());
}
} ///:~For the HashMap, the
entrySet( ) method produces a Set of Map.entry
objects, which contain both the key and the value for each entry, so you see
both of them printed.
Note that PrintData.print( )
takes advantage of the fact that the objects in these containers are of class
Object so the call toString( ) by
System.out.println( ) is automatic. It’s more likely that in
your problem, you must make the assumption that your Iterator is walking
through a container of some specific type. For example, you might assume that
everything in the container is a Shape with a draw( ) method.
Then you must downcast from the Object that Iterator.next( )
returns to produce a Shape.
By now you should understand that there
are really only three container components: Map, List, and
Set, and only two or three implementations of each interface. If you need
to use the functionality offered by a particular interface, how do you
decide which particular implementation to use?
To understand the answer, you must be
aware that each different implementation has its own features, strengths, and
weaknesses. For example, you can see in the diagram that the
“feature” of Hashtable, Vector, and Stack is
that they are legacy classes, so that old code doesn’t break. On the other
hand, it’s best if you don’t use those for new (Java 2)
code.
The distinction between the other
containers often comes down to what they are “backed by”; that is,
the data structures that physically implement your desired interface.
This means that, for example, ArrayList and LinkedList implement
the List interface so your program will produce the same results
regardless of the one you use. However, ArrayList is backed by an array,
while the LinkedList is implemented in the usual way for a doubly linked
list, as individual objects each containing data along with references to the
previous and next elements in the list. Because of this, if you want to do many
insertions and removals in the middle of a list, a LinkedList is the
appropriate choice. (LinkedList also has additional functionality that is
established in AbstractSequentialList.) If not,
an ArrayList is typically faster.
As another example, a Set can be
implemented as either a TreeSet or a HashSet. A TreeSet is
backed by a TreeMap and is designed to produce a constantly sorted set.
However, if you’re going to have larger quantities in your Set, the
performance of TreeSet insertions will get slow. When you’re
writing a program that needs a Set, you should choose HashSet by
default, and change to TreeSet when it's more important to have a
constantly sorted set.
The most convincing way to see the
differences between the implementations of List is with a performance
test. The following code establishes an inner base class to use as a test
framework, then creates an array of
anonymous
inner classes, one for each different test. Each of these inner classes is
called by the test( ) method. This approach allows you to easily add
and remove new kinds of tests.
//: c09:ListPerformance.java
// Demonstrates performance differences in Lists.
import java.util.*;
import com.bruceeckel.util.*;
public class ListPerformance {
private abstract static class Tester {
String name;
int size; // Test quantity
Tester(String name, int size) {
this.name = name;
this.size = size;
}
abstract void test(List a, int reps);
}
private static Tester[] tests = {
new Tester("get", 300) {
void test(List a, int reps) {
for(int i = 0; i < reps; i++) {
for(int j = 0; j < a.size(); j++)
a.get(j);
}
}
},
new Tester("iteration", 300) {
void test(List a, int reps) {
for(int i = 0; i < reps; i++) {
Iterator it = a.iterator();
while(it.hasNext())
it.next();
}
}
},
new Tester("insert", 5000) {
void test(List a, int reps) {
int half = a.size()/2;
String s = "test";
ListIterator it = a.listIterator(half);
for(int i = 0; i < size * 10; i++)
it.add(s);
}
},
new Tester("remove", 5000) {
void test(List a, int reps) {
ListIterator it = a.listIterator(3);
while(it.hasNext()) {
it.next();
it.remove();
}
}
},
};
public static void test(List a, int reps) {
// A trick to print out the class name:
System.out.println("Testing " +
a.getClass().getName());
for(int i = 0; i < tests.length; i++) {
Collections2.fill(a,
Collections2.countries.reset(),
tests[i].size);
System.out.print(tests[i].name);
long t1 = System.currentTimeMillis();
tests[i].test(a, reps);
long t2 = System.currentTimeMillis();
System.out.println(": " + (t2 - t1));
}
}
public static void testArray(int reps) {
System.out.println("Testing array as List");
// Can only do first two tests on an array:
for(int i = 0; i < 2; i++) {
String[] sa = new String[tests[i].size];
Arrays2.fill(sa,
Collections2.countries.reset());
List a = Arrays.asList(sa);
System.out.print(tests[i].name);
long t1 = System.currentTimeMillis();
tests[i].test(a, reps);
long t2 = System.currentTimeMillis();
System.out.println(": " + (t2 - t1));
}
}
public static void main(String[] args) {
int reps = 50000;
// Or, choose the number of repetitions
// via the command line:
if(args.length > 0)
reps = Integer.parseInt(args[0]);
System.out.println(reps + " repetitions");
testArray(reps);
test(new ArrayList(), reps);
test(new LinkedList(), reps);
test(new Vector(), reps);
}
} ///:~The inner class Tester is
abstract, to provide a base class for the specific tests. It contains a
String to be printed when the test starts, a size parameter to be
used by the test for quantity of elements or repetitions of tests, a constructor
to initialize the fields, and an abstract method test( ) that
does the work. All the different types of tests are collected in one place, the
array tests, which is initialized with different anonymous inner classes
that inherit from Tester. To add or remove tests, simply add or remove an
inner class definition from the array, and everything else happens
automatically.
To compare array access to container
access (primarily against ArrayList), a special test is created for
arrays by wrapping one as a List using Arrays.asList( ). Note
that only the first two tests can be performed in this case, because you cannot
insert or remove elements from an array.
The List that’s handed to
test( ) is first filled with elements, then each test in the
tests array is timed. The results will vary from machine to machine; they
are intended to give only an order of magnitude comparison between the
performance of the different containers. Here is a summary of one
run:
|
Type |
Get |
Iteration |
Insert |
Remove |
|
array |
1430 |
3850 |
na |
na |
|
ArrayList |
3070 |
12200 |
500 |
46850 |
|
LinkedList |
16320 |
9110 |
110 |
60 |
|
Vector |
4890 |
16250 |
550 |
46850 |
As expected, arrays are faster than any
container for random-access lookups and iteration. You can see that random
accesses (get( )) are cheap for ArrayLists and expensive for
LinkedLists. (Oddly, iteration is faster for a
LinkedList than an
ArrayList, which is a bit counterintuitive.) On
the other hand, insertions and removals from the middle of a list are
dramatically cheaper for a LinkedList than for an
ArrayList—especially removals.
Vector is generally not as fast as
ArrayList, and it should be avoided; it’s only in the library for
legacy code support (the only reason it works in this program is because it was
adapted to be a List in Java 2). The best approach is probably to
choose an ArrayList as your default, and to change to a LinkedList
if you discover performance problems due to many insertions and removals from
the middle of the list. And of course, if you are working with a fixed-sized
group of elements, use an array.
You can choose between a
TreeSet and a
HashSet, depending on the size of the
Set (if you need to produce an ordered sequence
from a Set, use TreeSet). The following test program gives
an indication of this trade-off:
//: c09:SetPerformance.java
import java.util.*;
import com.bruceeckel.util.*;
public class SetPerformance {
private abstract static class Tester {
String name;
Tester(String name) { this.name = name; }
abstract void test(Set s, int size, int reps);
}
private static Tester[] tests = {
new Tester("add") {
void test(Set s, int size, int reps) {
for(int i = 0; i < reps; i++) {
s.clear();
Collections2.fill(s,
Collections2.countries.reset(),size);
}
}
},
new Tester("contains") {
void test(Set s, int size, int reps) {
for(int i = 0; i < reps; i++)
for(int j = 0; j < size; j++)
s.contains(Integer.toString(j));
}
},
new Tester("iteration") {
void test(Set s, int size, int reps) {
for(int i = 0; i < reps * 10; i++) {
Iterator it = s.iterator();
while(it.hasNext())
it.next();
}
}
},
};
public static void
test(Set s, int size, int reps) {
System.out.println("Testing " +
s.getClass().getName() + " size " + size);
Collections2.fill(s,
Collections2.countries.reset(), size);
for(int i = 0; i < tests.length; i++) {
System.out.print(tests[i].name);
long t1 = System.currentTimeMillis();
tests[i].test(s, size, reps);
long t2 = System.currentTimeMillis();
System.out.println(": " +
((double)(t2 - t1)/(double)size));
}
}
public static void main(String[] args) {
int reps = 50000;
// Or, choose the number of repetitions
// via the command line:
if(args.length > 0)
reps = Integer.parseInt(args[0]);
// Small:
test(new TreeSet(), 10, reps);
test(new HashSet(), 10, reps);
// Medium:
test(new TreeSet(), 100, reps);
test(new HashSet(), 100, reps);
// Large:
test(new TreeSet(), 1000, reps);
test(new HashSet(), 1000, reps);
}
} ///:~The following table shows the results of
one run. (Of course, this will be different according to the computer and JVM
you are using; you should run the test yourself as well):
|
Type |
Test size |
Add |
Contains |
Iteration |
|
|
10 |
138.0 |
115.0 |
187.0 |
|
TreeSet |
100 |
189.5 |
151.1 |
206.5 |
|
|
1000 |
150.6 |
177.4 |
40.04 |
|
|
10 |
55.0 |
82.0 |
192.0 |
|
HashSet |
100 |
45.6 |
90.0 |
202.2 |
|
|
1000 |
36.14 |
106.5 |
39.39 |
The performance of HashSet is
generally superior to TreeSet for all operations (but in particular
addition and lookup, the two most important operations). The only reason
TreeSet exists is because it maintains its elements in sorted order, so
you only use it when you need a sorted
Set.
When choosing between implementations of
Map, the size of the Map is what most
strongly affects performance, and the following test program gives an indication
of this trade-off:
//: c09:MapPerformance.java
// Demonstrates performance differences in Maps.
import java.util.*;
import com.bruceeckel.util.*;
public class MapPerformance {
private abstract static class Tester {
String name;
Tester(String name) { this.name = name; }
abstract void test(Map m, int size, int reps);
}
private static Tester[] tests = {
new Tester("put") {
void test(Map m, int size, int reps) {
for(int i = 0; i < reps; i++) {
m.clear();
Collections2.fill(m,
Collections2.geography.reset(), size);
}
}
},
new Tester("get") {
void test(Map m, int size, int reps) {
for(int i = 0; i < reps; i++)
for(int j = 0; j < size; j++)
m.get(Integer.toString(j));
}
},
new Tester("iteration") {
void test(Map m, int size, int reps) {
for(int i = 0; i < reps * 10; i++) {
Iterator it = m.entrySet().iterator();
while(it.hasNext())
it.next();
}
}
},
};
public static void
test(Map m, int size, int reps) {
System.out.println("Testing " +
m.getClass().getName() + " size " + size);
Collections2.fill(m,
Collections2.geography.reset(), size);
for(int i = 0; i < tests.length; i++) {
System.out.print(tests[i].name);
long t1 = System.currentTimeMillis();
tests[i].test(m, size, reps);
long t2 = System.currentTimeMillis();
System.out.println(": " +
((double)(t2 - t1)/(double)size));
}
}
public static void main(String[] args) {
int reps = 50000;
// Or, choose the number of repetitions
// via the command line:
if(args.length > 0)
reps = Integer.parseInt(args[0]);
// Small:
test(new TreeMap(), 10, reps);
test(new HashMap(), 10, reps);
test(new Hashtable(), 10, reps);
// Medium:
test(new TreeMap(), 100, reps);
test(new HashMap(), 100, reps);
test(new Hashtable(), 100, reps);
// Large:
test(new TreeMap(), 1000, reps);
test(new HashMap(), 1000, reps);
test(new Hashtable(), 1000, reps);
}
} ///:~Because the size of the map is the issue,
you’ll see that the timing tests divide the time by the size to normalize
each measurement. Here is one set of results. (Yours will probably be
different.)
|
Type |
Test size |
Put |
Get |
Iteration |
|---|---|---|---|---|
|
|
10 |
143.0 |
110.0 |
186.0 |
|
TreeMap |
100 |
201.1 |
188.4 |
280.1 |
|
|
1000 |
222.8 |
205.2 |
40.7 |
|
|
10 |
66.0 |
83.0 |
197.0 |
|
HashMap |
100 |
80.7 |
135.7 |
278.5 |
|
|
1000 |
48.2 |
105.7 |
41.4 |
|
|
10 |
61.0 |
93.0 |
302.0 |
|
Hashtable |
100 |
90.6 |
143.3 |
329.0 |
|
|
1000 |
54.1 |
110.95 |
47.3 |
As you might expect,
Hashtable performance is roughly equivalent to
HashMap. (You can also see that HashMap is generally a bit faster.
HashMap is intended to replace Hashtable.) The
TreeMap is generally slower than the
HashMap, so why would you use it? So you could use it not as a
Map, but as a way to create an ordered list. The behavior of a
tree is such that it’s always in order and doesn’t have to be
specially sorted. Once you fill a TreeMap, you can call
keySet( ) to get a Set view of the
keys, then toArray( ) to produce an array of
those keys. You can then use the static method
Arrays.binarySearch( ) (discussed later) to rapidly find objects in
your sorted array. Of course, you would probably only do this if, for some
reason, the behavior of a HashMap was unacceptable, since HashMap
is designed to rapidly find things. Also, you can easily create a HashMap
from a TreeMap with a single object creation In the end, when
you’re using a Map your first choice should be HashMap, and
only if you need a constantly sorted Map will you need
TreeMap.
Utilities to perform sorting and
searching for Lists have the same names and
signatures as those for sorting arrays of objects, but are static methods
of Collections instead of Arrays.
Here’s an example, modified from
ArraySearching.java:
//: c09:ListSortSearch.java
// Sorting and searching Lists with 'Collections.'
import com.bruceeckel.util.*;
import java.util.*;
public class ListSortSearch {
public static void main(String[] args) {
List list = new ArrayList();
Collections2.fill(list,
Collections2.capitals, 25);
System.out.println(list + "\n");
Collections.shuffle(list);
System.out.println("After shuffling: "+list);
Collections.sort(list);
System.out.println(list + "\n");
Object key = list.get(12);
int index =
Collections.binarySearch(list, key);
System.out.println("Location of " + key +
" is " + index + ", list.get(" +
index + ") = " + list.get(index));
AlphabeticComparator comp =
new AlphabeticComparator();
Collections.sort(list, comp);
System.out.println(list + "\n");
key = list.get(12);
index =
Collections.binarySearch(list, key, comp);
System.out.println("Location of " + key +
" is " + index + ", list.get(" +
index + ") = " + list.get(index));
}
} ///:~The use of these methods is identical to
the ones in Arrays, but you’re using a List instead of an
array. Just like searching and sorting with arrays, if you sort using a
Comparator you must binarySearch( ) using the same
Comparator.
This program also demonstrates the
shuffle( ) method in Collections,
which randomizes the order of a
List.
|
enumeration(Collection)
|
Produces an old-style Enumeration
for the argument. |
|
max(Collection) min(Collection) |
Produces the maximum or minimum element
in the argument using the natural comparison method of the objects in the
Collection. |
|
max(Collection, Comparator)
min(Collection,
Comparator) |
Produces the maximum or minimum element
in the Collection using the Comparator. |
|
reverse( ) |
Reverses all the elements in
place. |
|
copy(List dest, List
src) |
Copies elements from src to
dest. |
|
fill(List list, Object
o) |
Replaces all the elements of list with
o. |
|
nCopies(int n, Object o)
|
Returns an immutable List of size
n whose references all point to o. |
Note that min( ) and
max( ) work with Collection objects, not with Lists,
so you don’t need to worry about whether the Collection should be
sorted or not. (As mentioned earlier, you do need to sort( )
a List or an array before performing a
binarySearch( ).)
Often it is convenient to create a
read-only version of a Collection or Map. The Collections
class allows you to do this by passing the original container into a method that
hands back a read-only version. There are four variations on this method, one
each for Collection (if you don’t want to treat a Collection
as a more specific type), List, Set, and Map. This
example shows the proper way to build read-only versions of
each:
//: c09:ReadOnly.java
// Using the Collections.unmodifiable methods.
import java.util.*;
import com.bruceeckel.util.*;
public class ReadOnly {
static Collections2.StringGenerator gen =
Collections2.countries;
public static void main(String[] args) {
Collection c = new ArrayList();
Collections2.fill(c, gen, 25); // Insert data
c = Collections.unmodifiableCollection(c);
System.out.println(c); // Reading is OK
c.add("one"); // Can't change it
List a = new ArrayList();
Collections2.fill(a, gen.reset(), 25);
a = Collections.unmodifiableList(a);
ListIterator lit = a.listIterator();
System.out.println(lit.next()); // Reading OK
lit.add("one"); // Can't change it
Set s = new HashSet();
Collections2.fill(s, gen.reset(), 25);
s = Collections.unmodifiableSet(s);
System.out.println(s); // Reading OK
//! s.add("one"); // Can't change it
Map m = new HashMap();
Collections2.fill(m,
Collections2.geography, 25);
m = Collections.unmodifiableMap(m);
System.out.println(m); // Reading OK
//! m.put("Ralph", "Howdy!");
}
} ///:~In each case, you must fill the container
with meaningful data before you make it read-only. Once it is loaded, the
best approach is to replace the existing reference with the reference that is
produced by the “unmodifiable” call. That way, you don’t run
the risk of accidentally changing the contents once you’ve made it
unmodifiable. On the other hand, this tool also allows you to keep a modifiable
container as private within a class and to return a read-only reference
to that container from a method call. So you can change it from within the
class, but everyone else can only read it.
Calling the “unmodifiable”
method for a particular type does not cause compile-time checking, but once the
transformation has occurred, any calls to methods that modify the contents of a
particular container will produce an
UnsupportedOperationException.
The
synchronized keyword is an important part of the
subject of multithreading, a more complicated
topic that will not be introduced until Chapter 14. Here, I shall note only that
the Collections class contains a way to automatically synchronize an
entire container. The syntax is similar to the “unmodifiable”
methods:
//: c09:Synchronization.java
// Using the Collections.synchronized methods.
import java.util.*;
public class Synchronization {
public static void main(String[] args) {
Collection c =
Collections.synchronizedCollection(
new ArrayList());
List list = Collections.synchronizedList(
new ArrayList());
Set s = Collections.synchronizedSet(
new HashSet());
Map m = Collections.synchronizedMap(
new HashMap());
}
} ///:~In this case, you immediately pass the
new container through the appropriate “synchronized” method; that
way there’s no chance of accidentally exposing the unsynchronized
version.
The Java containers also have a mechanism
to prevent more than one process from modifying the contents of a container. The
problem occurs if you’re iterating through a container and some other
process steps in and inserts, removes, or changes an object in that container.
Maybe you’ve already passed that object, maybe it’s ahead of you,
maybe the size of the container shrinks after you call
size( )—there are many scenarios for disaster. The Java
containers library incorporates a fail-fast mechanism that looks for any
changes to the container other than the ones your process is personally
responsible for. If it detects that someone else is modifying the container, it
immediately produces a ConcurrentModificationException. This is the
“fail-fast” aspect—it doesn’t try to detect a problem
later on using a more complex
algorithm.
It’s possible to turn an array into
a List with the Arrays.asList( ) method:
//: c09:Unsupported.java
// Sometimes methods defined in the
// Collection interfaces don't work!
import java.util.*;
public class Unsupported {
private static String[] s = {
"one", "two", "three", "four", "five",
"six", "seven", "eight", "nine", "ten",
};
static List a = Arrays.asList(s);
static List a2 = a.subList(3, 6);
public static void main(String[] args) {
System.out.println(a);
System.out.println(a2);
System.out.println(
"a.contains(" + s[0] + ") = " +
a.contains(s[0]));
System.out.println(
"a.containsAll(a2) = " +
a.containsAll(a2));
System.out.println("a.isEmpty() = " +
a.isEmpty());
System.out.println(
"a.indexOf(" + s[5] + ") = " +
a.indexOf(s[5]));
// Traverse backwards:
ListIterator lit = a.listIterator(a.size());
while(lit.hasPrevious())
System.out.print(lit.previous() + " ");
System.out.println();
// Set the elements to different values:
for(int i = 0; i < a.size(); i++)
a.set(i, "47");
System.out.println(a);
// Compiles, but won't run:
lit.add("X"); // Unsupported operation
a.clear(); // Unsupported
a.add("eleven"); // Unsupported
a.addAll(a2); // Unsupported
a.retainAll(a2); // Unsupported
a.remove(s[0]); // Unsupported
a.removeAll(a2); // Unsupported
}
} ///:~You’ll discover that only a portion
of the Collection and List interfaces are actually implemented.
The rest of the methods cause the unwelcome appearance of something called an
UnsupportedOperationException. You’ll learn all about exceptions in
the next chapter, but the short story is that the Collection
interface—as well as some of the other interfaces in the
Java containers library—contain “optional” methods, which
might or might not be “supported” in the concrete class that
implements that interface. Calling an unsupported method causes an
UnsupportedOperationException to indicate a programming
error.
“What?!?” you say,
incredulous. “The whole point of interfaces and base classes is
that they promise these methods will do something meaningful! This breaks that
promise—it says that not only will calling some methods not perform
a meaningful behavior, they will stop the program! Type safety was just thrown
out the window!”
It’s not quite that bad. With a
Collection, List, Set, or Map, the compiler still
restricts you to calling only the methods in that interface, so
it’s not like Smalltalk (in which you can call any method for any object,
and find out only when you run the program whether your call does anything). In
addition, most methods that take a Collection as an argument only read
from that Collection—all the “read” methods of
Collection are not optional.
This approach prevents an explosion of
interfaces in the design. Other designs for container libraries always seem to
end up with a confusing plethora of interfaces to describe each of the
variations on the main theme and are thus difficult to learn. It’s not
even possible to capture all of the special cases in interfaces, because
someone can always invent a new interface. The “unsupported
operation” approach achieves an important goal of the Java containers
library: the containers are simple to learn and use; unsupported operations are
a special case that can be learned later. For this approach to work,
however:
In the example above,
Arrays.asList( ) produces a List that
is backed by a fixed-size array. Therefore it makes sense that the only
supported operations are the ones that don’t change the size of the array.
If, on the other hand, a new interface were required to express this
different kind of behavior (called, perhaps,
“FixedSizeList”), it would throw open the door to complexity
and soon you wouldn’t know where to start when trying to use the
library.
The documentation for a method that takes
a Collection, List, Set, or Map as an argument
should specify which of the optional methods must be implemented. For example,
sorting requires the set( ) and Iterator.set( ) methods,
but not add( ) and remove( ).
Unfortunately, a lot of code was written
using the Java 1.0/1.1 containers, and even new code is sometimes written using
these classes. So although you should never use the old containers when writing
new code, you’ll still need to be aware of them. However, the old
containers were quite limited, so there’s not that much to say about them.
(Since they are in the past, I will try to refrain from overemphasizing some of
the hideous design
decisions.)
The only self-expanding sequence in Java
1.0/1.1 was the Vector, and so it saw a lot of
use. Its flaws are too numerous to describe here (see the first edition of this
book, available on this book’s CD ROM and as a free download from
www.BruceEckel.com). Basically, you can think of it as an
ArrayList with long, awkward method names. In the Java 2 container
library, Vector was adapted so that it could fit as a Collection
and a List, so in the following example the
Collections2.fill( ) method is successfully used. This turns out to
be a bit perverse, as it may confuse some people into thinking that
Vector has gotten better, when it is actually included only to support
pre-Java 2 code.
The Java 1.0/1.1 version of the iterator
chose to invent a new name, “enumeration,” instead of using a term
that everyone was already familiar with. The
Enumeration interface is smaller than
Iterator, with only two methods, and it uses longer method names:
boolean hasMoreElements( ) produces true if this
enumeration contains more elements, and Object nextElement( )
returns the next element of this enumeration if there are any more
(otherwise it throws an exception).
Enumeration is only an interface,
not an implementation, and even new libraries sometimes still use the old
Enumeration—which is unfortunate but generally harmless. Even
though you should always use Iterator when you can in your own code, you
must be prepared for libraries that want to hand you an
Enumeration.
In addition, you
can produce an Enumeration for any Collection by using the
Collections.enumeration( ) method, as seen in this
example:
//: c09:Enumerations.java
// Java 1.0/1.1 Vector and Enumeration.
import java.util.*;
import com.bruceeckel.util.*;
class Enumerations {
public static void main(String[] args) {
Vector v = new Vector();
Collections2.fill(
v, Collections2.countries, 100);
Enumeration e = v.elements();
while(e.hasMoreElements())
System.out.println(e.nextElement());
// Produce an Enumeration from a Collection:
e = Collections.enumeration(new ArrayList());
}
} ///:~The Java 1.0/1.1 Vector has only
an addElement( ) method, but fill( ) uses the
add( ) method that was pasted on as Vector was turned into a
List. To produce an Enumeration, you call elements( ),
then you can use it to perform a forward iteration.
The last line creates an ArrayList
and uses enumeration( ) to adapt an Enumeration from the
ArrayList Iterator. Thus, if you have old code that wants an
Enumeration, you can still use the new
containers.
As you’ve seen in the performance
comparison in this chapter, the basic Hashtable
is very similar to the HashMap, even down to the method names.
There’s no reason to use Hashtable instead of HashMap in new
code.
The concept of the stack was introduced
earlier, with the LinkedList. What’s rather odd about the
Java 1.0/1.1 Stack is that instead of using a
Vector as a building block,
Stack is inherited from Vector. So
it has all of the characteristics and behaviors of a Vector plus some
extra Stack behaviors. It’s difficult to know whether the designers
explicitly decided that this was an especially useful way of doing things, or
whether it was just a naive design.
Here’s a simple demonstration of
Stack that pushes each line from a String array:
//: c09:Stacks.java
// Demonstration of Stack Class.
import java.util.*;
public class Stacks {
static String[] months = {
"January", "February", "March", "April",
"May", "June", "July", "August", "September",
"October", "November", "December" };
public static void main(String[] args) {
Stack stk = new Stack();
for(int i = 0; i < months.length; i++)
stk.push(months[i] + " ");
System.out.println("stk = " + stk);
// Treating a stack as a Vector:
stk.addElement("The last line");
System.out.println(
"element 5 = " + stk.elementAt(5));
System.out.println("popping elements:");
while(!stk.empty())
System.out.println(stk.pop());
}
} ///:~Each line in the months array is
inserted into the Stack with push( ), and later fetched from
the top of the stack with a pop( ). To make a point, Vector
operations are also performed on the Stack object. This is possible
because, by virtue of inheritance, a Stack is a Vector.
Thus, all operations that can be performed on a Vector can also be
performed on a Stack, such as elementAt( ).
A BitSet
is used if you want to efficiently store a lot of on-off information. It’s
efficient only from the standpoint of size; if you’re looking for
efficient access, it is slightly slower than using an array of some native
type.
In addition, the minimum size of the
BitSet is that of a long: 64 bits. This implies that if
you’re storing anything smaller, like 8 bits, a BitSet will be
wasteful; you’re better off creating your own class, or just an array, to
hold your flags if size is an issue.
A normal container expands as you add
more elements, and the BitSet does this as well. The following example
shows how the BitSet works:
//: c09:Bits.java
// Demonstration of BitSet.
import java.util.*;
public class Bits {
static void printBitSet(BitSet b) {
System.out.println("bits: " + b);
String bbits = new String();
for(int j = 0; j < b.size() ; j++)
bbits += (b.get(j) ? "1" : "0");
System.out.println("bit pattern: " + bbits);
}
public static void main(String[] args) {
Random rand = new Random();
// Take the LSB of nextInt():
byte bt = (byte)rand.nextInt();
BitSet bb = new BitSet();
for(int i = 7; i >=0; i--)
if(((1 << i) & bt) != 0)
bb.set(i);
else
bb.clear(i);
System.out.println("byte value: " + bt);
printBitSet(bb);
short st = (short)rand.nextInt();
BitSet bs = new BitSet();
for(int i = 15; i >=0; i--)
if(((1 << i) & st) != 0)
bs.set(i);
else
bs.clear(i);
System.out.println("short value: " + st);
printBitSet(bs);
int it = rand.nextInt();
BitSet bi = new BitSet();
for(int i = 31; i >=0; i--)
if(((1 << i) & it) != 0)
bi.set(i);
else
bi.clear(i);
System.out.println("int value: " + it);
printBitSet(bi);
// Test bitsets >= 64 bits:
BitSet b127 = new BitSet();
b127.set(127);
System.out.println("set bit 127: " + b127);
BitSet b255 = new BitSet(65);
b255.set(255);
System.out.println("set bit 255: " + b255);
BitSet b1023 = new BitSet(512);
b1023.set(1023);
b1023.set(1024);
System.out.println("set bit 1023: " + b1023);
}
} ///:~The random number generator is used to
create a random byte, short, and int, and each one is
transformed into a corresponding bit pattern in a BitSet. This works fine
because a BitSet is 64 bits, so none of these cause it to increase in
size. Then a BitSet of 512 bits is created. The constructor allocates
storage for twice that number of bits. However, you can still set bit 1024 or
greater.
To review the containers provided in the
standard Java library:
The
containers are tools that you can use on a day-to-day basis to make your
programs simpler, more powerful, and more
effective.
[45]
It’s possible, however, to ask how big the vector is, and the
at( ) method does perform bounds checking.
[46]
This is one of the places where C++ is distinctly superior to Java, since C++
supports parameterized types with the template
keyword.
[47]
The C++ programmer will note how much the code could be collapsed with the use
of default arguments and templates. The Python programmer will note that this
entire library would be largely unnecessary in that language.
[48]
By Joshua Bloch at Sun.
[49]
This data was found on the Internet, then processed by creating a Python program
(see www.Python.org).
[50]
This is a place where operator overloading would be nice.
[51]
If these speedups still don’t meet your performance needs, you can further
accelerate table lookup by writing your own Map and customizing it to
your particular types to avoid delays due to casting to and from Objects.
To reach even higher levels of performance, speed enthusiasts can use Donald
Knuth’s The Art of Computer Programming, Volume 3: Sorting and
Searching, Second Edition to replace overflow bucket lists with arrays that
have two additional benefits: they can be optimized for disk storage
characteristics and they can save most of the time of creating and garbage
collecting individual records.