9: Holding
Your Objects

It’s a fairly simple program that has only a fixed quantity of objects with known lifetimes.

In general, your programs will always be creating new objects based on some criteria that will be known only at the time the program is running. You won’t know until run-time the quantity or even the exact type of the objects you need. To solve the general programming problem, you need to be able to create any number of objects, anytime, anywhere. So you can’t rely on creating a named reference to hold each one of your objects:

since you’ll never know how many of these you’ll actually need.

To solve this rather essential problem, Java has several ways to hold objects (or rather, references to objects). The built-in type is the array, which has been discussed before. Also, the Java utilities library has a reasonably complete set of container classes (also known as collection classes, but because the Java 2 libraries use the name Collection to refer to a particular subset of the library, I shall use the more inclusive term “container”). Containers provide sophisticated ways to hold and even manipulate your objects.

Most of the necessary introduction to arrays is in the last section of Chapter 4, which showed how you define and initialize an array. Holding objects is the focus of this chapter, and an array is just one way to hold objects. But there are a number of other ways to hold objects, so what makes an array special?

There are two issues that distinguish arrays from other types of containers: efficiency and type. The array is the most efficient way that Java provides to store and randomly access a sequence of objects (actually, object references). The array is a simple linear sequence, which makes element access fast, but you pay for this speed: when you create an array object, its size is fixed and cannot be changed for the lifetime of that array object. You might suggest creating an array of a particular size and then, if you run out of space, creating a new one and moving all the references from the old one to the new one. This is the behavior of the ArrayList class, which will be studied later in this chapter. However, because of the overhead of this size flexibility, an ArrayList is measurably less efficient than an array.

The vector container class in C++ does know the type of objects it holds, but it has a different drawback when compared with arrays in Java: the C++ vector’s operator[] doesn’t do bounds checking, so you can run past the end[45]. In Java, you get bounds checking regardless of whether you’re using an array or a container—you’ll get a RuntimeException if you exceed the bounds. As you’ll learn in Chapter 10, this type of exception indicates a programmer error, and thus you don’t need to check for it in your code. As an aside, the reason the C++ vector doesn’t check bounds with every access is speed—in Java you have the constant performance overhead of bounds checking all the time for both arrays and containers.

The other generic container classes that will be studied in this chapter, List, Set, and Map, all deal with objects as if they had no specific type. That is, they treat them as type Object, the root class of all classes in Java. This works fine from one standpoint: you need to build only one container, and any Java object will go into that container. (Except for primitives—these can be placed in containers as constants using the Java primitive wrapper classes, or as changeable values by wrapping in your own class.) This is the second place where an array is superior to the generic containers: when you create an array, you create it to hold a specific type. This means that you get compile-time type checking to prevent you from putting the wrong type in, or mistaking the type that you’re extracting. Of course, Java will prevent you from sending an inappropriate message to an object, either at compile-time or at run-time. So it’s not much riskier one way or the other, it’s just nicer if the compiler points it out to you, faster at run-time, and there’s less likelihood that the end user will get surprised by an exception.

For efficiency and type checking it’s always worth trying to use an array if you can. However, when you’re trying to solve a more general problem arrays can be too restrictive. After looking at arrays, the rest of this chapter will be devoted to the container classes provided by Java.

Regardless of what type of array you’re working with, the array identifier is actually a reference to a true object that’s created on the heap. This is the object that holds the references to the other objects, and it can be created either implicitly, as part of the array initialization syntax, or explicitly with a new expression. Part of the array object (in fact, the only field or method you can access) is the read-only length member that tells you how many elements can be stored in that array object. The ‘[]’ syntax is the only other access that you have to the array object.

The following example shows the various ways that an array can be initialized, and how the array references can be assigned to different array objects. It also shows that arrays of objects and arrays of primitives are almost identical in their use. The only difference is that arrays of objects hold references, while arrays of primitives hold the primitive values directly.

Here’s the output from the program:

The array a is initially just a null reference, and the compiler prevents you from doing anything with this reference until you’ve properly initialized it. The array b is initialized to point to an array of Weeble references, but no actual Weeble objects are ever placed in that array. However, you can still ask what the size of the array is, since b is pointing to a legitimate object. This brings up a slight drawback: you can’t find out how many elements are actually in the array, since length tells you only how many elements can be placed in the array; that is, the size of the array object, not the number of elements it actually holds. However, when an array object is created its references are automatically initialized to null, so you can see whether a particular array slot has an object in it by checking to see whether it’s null. Similarly, an array of primitives is automatically initialized to zero for numeric types, (char)0 for char, and false for boolean.

Array c shows the creation of the array object followed by the assignment of Weeble objects to all the slots in the array. Array d shows the “aggregate initialization” syntax that causes the array object to be created (implicitly with new on the heap, just like for array c) and initialized with Weeble objects, all in one statement.

The next array initialization could be thought of as a “dynamic aggregate initialization.” The aggregate initialization used by d must be used at the point of d’s definition, but with the second syntax you can create and initialize an array object anywhere. For example, suppose hide( ) is a method that takes an array of Weeble objects. You could call it by saying:

but you can also dynamically create the array you want to pass as the argument:

In some situations this new syntax provides a more convenient way to write code.

The expression

shows how you can take a reference that’s attached to one array object and assign it to another array object, just as you can do with any other type of object reference. Now both a and d are pointing to the same array object on the heap.

The second part of ArraySize.java shows that primitive arrays work just like object arrays except that primitive arrays hold the primitive values directly.

Container classes can hold only references to objects. An array, however, can be created to hold primitives directly, as well as references to objects. It is possible to use the “wrapper” classes such as Integer, Double, etc. to place primitive values inside a container, but the wrapper classes for primitives can be awkward to use. In addition, it’s much more efficient to create and access an array of primitives than a container of wrapped primitives.

Of course, if you’re using a primitive type and you need the flexibility of a container that automatically expands when more space is needed, the array won’t work and you’re forced to use a container of wrapped primitives. You might think that there should be a specialized type of ArrayList for each of the primitive data types, but Java doesn’t provide this for you. Some sort of templatizing mechanism might someday provide a better way for Java to handle this problem.[46]

Suppose you’re writing a method and you don’t just want to return just one thing, but a whole bunch of things. Languages like C and C++ make this difficult because you can’t just return an array, only a pointer to an array. This introduces problems because it becomes messy to control the lifetime of the array, which easily leads to memory leaks.

Java takes a similar approach, but you just “return an array.” Actually, of course, you’re returning a reference to an array, but with Java you never worry about responsibility for that array—it will be around as long as you need it, and the garbage collector will clean it up when you’re done.

As an example, consider returning an array of String:

The method flavorSet( ) creates an array of String called results. The size of this array is n, determined by the argument you pass into the method. Then it proceeds to choose flavors randomly from the array flav and place them into results, which it finally returns. Returning an array is just like returning any other object—it’s a reference. It’s not important that the array was created within flavorSet( ), or that the array was created anyplace else, for that matter. The garbage collector takes care of cleaning up the array when you’re done with it, and the array will persist for as long as you need it.

As an aside, notice that when flavorSet( ) chooses flavors randomly, it ensures that a random choice hasn’t been picked before. This is performed in a do loop that keeps making random choices until it finds one that’s not already in the picked array. (Of course, a String comparison could also have been performed to see if the random choice was already in the results array, but String comparisons are inefficient.) If it’s successful, it adds the entry and finds the next one (i gets incremented).

main( ) prints out 20 full sets of flavors, so you can see that flavorSet( ) chooses the flavors in a random order each time. It’s easiest to see this if you redirect the output into a file. And while you’re looking at the file, remember, you just want the ice cream, you don’t need it.

In java.util, you’ll find the Arrays class, which holds a set of static methods that perform utility functions for arrays. There are four basic functions: equals( ), to compare two arrays for equality; fill( ), to fill an array with a value; sort( ), to sort the array; and binarySearch( ), to find an element in a sorted array. All of these methods are overloaded for all the primitive types and Objects. In addition, there’s a single asList( ) method that takes any array and turns it into a List container—which you’ll learn about later in this chapter.

While useful, the Arrays class stops short of being fully functional. For example, it would be nice to be able to easily print the elements of an array without having to code a for loop by hand every time. And as you’ll see, the fill( ) method only takes a single value and places it in the array, so if you wanted—for example—to fill an array with randomly generated numbers, fill( ) is no help.

Thus it makes sense to supplement the Arrays class with some additional utilities, which will be placed in the package com.bruceeckel.util for convenience. These will print an array of any type, and fill an array with values or objects that are created by an object called a generator that you can define.

Because code needs to be created for each primitive type as well as Object, there’s a lot of nearly duplicated code[47]. For example, a “generator” interface is required for each type because the return type of next( ) must be different in each case:

Arrays2 contains a variety of print( ) functions, overloaded for each type. You can simply print an array, you can add a message before the array is printed, or you can print a range of elements within an array. The print( ) code is self-explanatory:

To fill an array of elements using a generator, the fill( ) method takes a reference to an appropriate generator interface, which has a next( ) method that will somehow produce an object of the right type (depending on how the interface is implemented). The fill( ) method simply calls next( ) until the desired range has been filled. Now you can create any generator by implementing the appropriate interface, and use your generator with fill( ).

Random data generators are useful for testing, so a set of inner classes is created to implement all the primitive generator interfaces, as well as a String generator to represent Object. You can see that RandStringGenerator uses RandCharGenerator to fill an array of characters, which is then turned into a String. The size of the array is determined by the constructor argument.

To generate numbers that aren’t too large, RandIntGenerator defaults to a modulus of 10,000, but the overloaded constructor allows you to choose a smaller value.

Here’s a program to test the library, and to demonstrate how it is used:

The size parameter has a default value, but you can also set it from the command line.

The Java standard library Arrays also has a fill( ) method, but that is rather trivial—it only duplicates a single value into each location, or in the case of objects, copies the same reference into each location. Using Arrays2.print( ), the Arrays.fill( ) methods can be easily demonstrated:

You can either fill the entire array, or—as the last two statements show—a range of elements. But since you can only provide a single value to use for filling using Arrays.fill( ), the Arrays2.fill( ) methods produce much more interesting results.

The Java standard library provides a static method, System.arraycopy( ), which can make much faster copies of an array than if you use a for loop to perform the copy by hand. System.arraycopy( ) is overloaded to handle all types. Here’s an example that manipulates arrays of int:

The arguments to arraycopy( ) are the source array, the offset into the source array from whence to start copying, the destination array, the offset into the destination array where the copying begins, and the number of elements to copy. Naturally, any violation of the array boundaries will cause an exception.

The example shows that both primitive arrays and object arrays can be copied. However, if you copy arrays of objects then only the references get copied—there’s no duplication of the objects themselves. This is called a shallow copy (see Appendix A).

Arrays provides the overloaded method equals( ) to compare entire arrays for equality. Again, these are overloaded for all the primitives, and for Object. To be equal, the arrays must have the same number of elements and each element must be equivalent to each corresponding element in the other array, using the equals( ) for each element. (For primitives, that primitive’s wrapper class equals( ) is used; for example, Integer.equals( ) for int.) Here’s an example:

Originally, a1 and a2 are exactly equal, so the output is “true,” but then one of the elements is changed so the second line of output is “false.” In the last case, all the elements of s1 point to the same object, but s2 has five unique objects. However, array equality is based on contents (via Object.equals( )) and so the result is “true.”

One of the missing features in the Java 1.0 and 1.1 libraries is algorithmic operations—even simple sorting. This was a rather confusing situation to someone expecting an adequate standard library. Fortunately, Java 2 remedies the situation, at least for the sorting problem.

A problem with writing generic sorting code is that sorting must perform comparisons based on the actual type of the object. Of course, one approach is to write a different sorting method for every different type, but you should be able to recognize that this does not produce code that is easily reused for new types.

A primary goal of programming design is to “separate things that change from things that stay the same,” and here, the code that stays the same is the general sort algorithm, but the thing that changes from one use to the next is the way objects are compared. So instead of hard-wiring the comparison code into many different sort routines, the technique of the callback is used. With a callback, the part of the code that varies from case to case is encapsulated inside its own class, and the part of the code that’s always the same will call back to the code that changes. That way you can make different objects to express different ways of comparison and feed them to the same sorting code.

In Java 2, there are two ways to provide comparison functionality. The first is with the natural comparison method that is imparted to a class by implementing the java.lang.Comparable interface. This is a very simple interface with a single method, compareTo( ). This method takes another Object as an argument, and produces a negative value if the argument is less than the current object, zero if the argument is equal, and a positive value if the argument is greater than the current object.

Here’s a class that implements Comparable and demonstrates the comparability by using the Java standard library method Arrays.sort( ):

When you define the comparison function, you are responsible for deciding what it means to compare one of your objects to another. Here, only the i values are used in the comparison, and the j values are ignored.

The static randInt( ) method produces positive values between zero and 100, and the generator( ) method produces an object that implements the Generator interface, by creating an anonymous inner class (see Chapter 8). This builds CompType objects by initializing them with random values. In main( ), the generator is used to fill an array of CompType, which is then sorted. If Comparable hadn’t been implemented, then you’d get a compile-time error message when you tried to call sort( ).

Now suppose someone hands you a class that doesn’t implement Comparable, or they hand you this class that does implement Comparable, but you decide you don’t like the way it works and would rather have a different comparison function for the type. To do this, you use the second approach for comparing objects, by creating a separate class that implements an interface called Comparator. This has two methods, compare( ) and equals( ). However, you don’t have to implement equals( ) except for special performance needs, because anytime you create a class it is implicitly inherited from Object, which has an equals( ). So you can just use the default Object equals( ) and satisfy the contract imposed by the interface.

The Collections class (which we’ll look at more later) contains a single Comparator that reverses the natural sorting order. This can easily be applied to the CompType:

The call to Collections.reverseOrder( ) produces the reference to the Comparator.

As a second example, the following Comparator compares CompType objects based on their j values rather than their i values:

The compare( ) method must return a negative integer, zero, or a positive integer if the first argument is less than, equal to, or greater than the second, respectively.

With the built-in sorting methods, you can sort any array of primitives, and any array of objects that either implements Comparable or has an associated Comparator. This fills a big hole in the Java libraries—believe it or not, there was no support in Java 1.0 or 1.1 for sorting Strings! Here’s an example that generates random String objects and sorts them:

One thing you’ll notice about the output in the String sorting algorithm is that it’s lexicographic, so it puts all the words starting with uppercase letters first, followed by all the words starting with lowercase letters. (Telephone books are typically sorted this way.) You may also want to group the words together regardless of case, and you can do this by defining a Comparator class, thereby overriding the default String Comparable behavior. For reuse, this will be added to the “util” package:

Each String is converted to lowercase before the comparison. String’s built-in compareTo( ) method provides the desired functionality.

Here’s a test using AlphabeticComparator:

The sorting algorithm that’s used in the Java standard library is designed to be optimal for the particular type you’re sorting—a Quicksort for primitives, and a stable merge sort for objects. So you shouldn’t need to spend any time worrying about performance unless your profiling tool points you to the sorting process as a bottleneck.

Once an array is sorted, you can perform a fast search for a particular item using Arrays.binarySearch( ). However, it’s very important that you do not try to use binarySearch( ) on an unsorted array; the results will be unpredictable. The following example uses a RandIntGenerator to fill an array, then to produces values to search for:

In the while loop, random values are generated as search items, until one of them is found.

Arrays.binarySearch( ) produces a value greater than or equal to zero if the search item is found. Otherwise, it produces a negative value representing the place that the element should be inserted if you are maintaining the sorted array by hand. The value produced is

The insertion point is the index of the first element greater than the key, or a.size( ), if all elements in the array are less than the specified key.

If the array contains duplicate elements, there is no guarantee which one will be found. The algorithm is thus not really designed to support duplicate elements, as much as tolerate them. If you need a sorted list of nonduplicated elements, however, use a TreeSet, which will be introduced later in this chapter. This takes care of all the details for you automatically. Only in cases of performance bottlenecks should you replace the TreeSet with a hand-maintained array.

If you have sorted an object array using a Comparator (primitive arrays do not allow sorting with a Comparator), you must include that same Comparator when you perform a binarySearch( ) (using the overloaded version of the function that’s provided). For example, the AlphabeticSorting.java program can be modified to perform a search:

The Comparator must be passed to the overloaded binarySearch( ) as the third argument. In the above example, success is guaranteed because the search item is plucked out of the array itself.

To summarize what you’ve seen so far, your first and most efficient choice to hold a group of objects should be an array, and you’re forced into this choice if you want to hold a group of primitives. In the remainder of this chapter we’ll look at the more general case, when you don’t know at the time you’re writing the program how many objects you’re going to need, or if you need a more sophisticated way to store your objects. Java provides a library of container classes to solve this problem, the basic types of which are List, Set, and Map. You can solve a surprising number of problems using these tools.

Among their other characteristics—Set, for example, holds only one object of each value, and Map is an associative array that lets you associate any object with any other object—the Java container classes will automatically resize themselves. So, unlike arrays, you can put in any number of objects and you don’t need to worry about how big to make the container while you’re writing the program.

To me, container classes are one of the most powerful tools for raw development because they significantly increase your programming muscle. The Java 2 containers represent a thorough redesign[48] of the rather poor showings in Java 1.0 and 1.1. Some of the redesign makes things tighter and more sensible. It also fills out the functionality of the containers library, providing the behavior of linked lists, queues, and deques (double-ended queues, pronounced “decks”).

The design of a containers library is difficult (true of most library design problems). In C++, the container classes covered the bases with many different classes. This was better than what was available prior to the C++ container classes (nothing), but it didn’t translate well into Java. On the other extreme, I’ve seen a containers library that consists of a single class, “container,” which acts like both a linear sequence and an associative array at the same time. The Java 2 container library strikes a balance: the full functionality that you expect from a mature container library, but easier to learn and use than the C++ container classes and other similar container libraries. The result can seem a bit odd in places. Unlike some of the decisions made in the early Java libraries, these oddities were not accidents, but carefully considered decisions based on trade-offs in complexity. It might take you a little while to get comfortable with some aspects of the library, but I think you’ll find yourself rapidly acquiring and using these new tools.

The Java 2 container library takes the issue of “holding your objects” and divides it into two distinct concepts:

We will first look at the general features of containers, then go into details, and finally learn why there are different versions of some containers, and how to choose between them.

Unlike arrays, the containers print nicely without any help. Here’s an example that also introduces you to the basic types of containers:

As mentioned before, there are two basic categories in the Java container library. The distinction is based on the number of items that are held in each location of the container. The Collection category only holds one item in each location (the name is a bit misleading since entire container libraries are often called “collections”). It includes the List, which holds a group of items in a specified sequence, and the Set, which only allows the addition of one item of each type. The ArrayList is a type of List, and HashSet is a type of Set. To add items to any Collection, there’s an add( ) method.

The Map holds key-value pairs, rather like a mini database. The above program uses one flavor of Map, the HashMap. If you have a Map that associates states with their capitals and you want to know the capital of Ohio, you look it up—almost as if you were indexing into an array. (Maps are also called associative arrays.) To add elements to a Map there’s a put( ) method that takes a key and a value as arguments. The above example only shows adding elements and does not look the elements up after they’re added. That will be shown later.

The fill( ) and mfill( ) methods fill Collections and Maps, respectively. If you look at the output, you can see that the default printing behavior (provided via the container’s various toString( ) methods) produces quite readable results, so no additional printing support is necessary as it was with arrays:

A Collection is printed surrounded by square braces, with each element separated by a comma. A Map is surrounded by curly braces, with each key and value associated with an equal sign (keys on the left, values on the right).

You can also immediately see the basic behavior of the different containers. The List holds the objects exactly as they are entered, without any reordering or editing. The Set, however, only accepts one of each object and it uses its own internal ordering method (in general, you are only concerned with whether or not something is a member of the Set, not the order in which it appears—for that you’d use a List). And the Map also only accepts one of each type of item, based on the key, and it also has its own internal ordering and does not care about the order in which you enter the items.

Although the problem of printing the containers is taken care of, filling containers suffers from the same deficiency as java.util.Arrays. Just like Arrays, there is a companion class called Collections containing static utility methods including one called fill( ). This fill( ) also just duplicates a single object reference throughout the container, and also only works for List objects and not Sets or Maps:

This method is made even less useful by the fact that it can only replace elements that are already in the List, and will not add new elements.

To be able to create interesting examples, here is a complementary Collections2 library (part of com.bruceeckel.util for convenience) with a fill( ) method that uses a generator to add elements, and allows you to specify the number of elements you want to add( ). The Generator interface defined previously will work for Collections, but the Map requires its own generator interface since a pair of objects (one key and one value) must be produced by each call to next( ). Here is the Pair class:

Next, the generator interface that produces the Pair:

With these, a set of utilities for working with the container classes can be developed:

Both versions of fill( ) take an argument that determines the number of items to add to the container. In addition, there are two generators for the map: RandStringPairGenerator, which creates any number of pairs of gibberish Strings with length determined by the constructor argument; and StringPairGenerator, which produces pairs of Strings given a two-dimensional array of String. The StringGenerator also takes a two-dimensional array of String but generates single items rather than Pairs. The static rsp, geography, countries, and capitals objects provide prebuilt generators, the last three using all the countries of the world and their capitals. Note that if you try to create more pairs than are available, the generators will loop around to the beginning, and if you are putting the pairs into a Map, the duplicates will just be ignored.

Here is the predefined dataset, which consists of country names and their capitals. It is set in a small font to prevent taking up unnecessary space:

This is simply a two-dimensional array of String data[49]. Here’s a simple test using the fill( ) methods and generators:

With these tools you can easily test the various containers by filling them with interesting data.

The “disadvantage” to using the Java containers is that you lose type information when you put an object into a container. This happens because the programmer of that container class had no idea what specific type you wanted to put in the container, and making the container hold only your type would prevent it from being a general-purpose tool. So instead, the container holds references to Object, which is the root of all the classes so it holds any type. (Of course, this doesn’t include primitive types, since they aren’t inherited from anything.) This is a great solution, except:

On the up side, Java won’t let you misuse the objects that you put into a container. If you throw a dog into a container of cats and then try to treat everything in the container as a cat, you’ll get a run-time exception when you pull the dog reference out of the cat container and try to cast it to a cat.

Here’s an example using the basic workhorse container, ArrayList. For starters, you can think of ArrayList as “an array that automatically expands itself.” Using an ArrayList is straightforward: create one, put objects in using add( ), and later get them out with get( ) using an index—just like you would with an array but without the square brackets[50]. ArrayList also has a method size( ) to let you know how many elements have been added so you don’t inadvertently run off the end and cause an exception.

First, Cat and Dog classes are created:

Cats and Dogs are placed into the container, then pulled out:

The classes Cat and Dog are distinct—they have nothing in common except that they are Objects. (If you don’t explicitly say what class you’re inheriting from, you automatically inherit from Object.) Since ArrayList holds Objects, you can not only put Cat objects into this container using the ArrayList method add( ), but you can also add Dog objects without complaint at either compile-time or run-time. When you go to fetch out what you think are Cat objects using the ArrayList method get( ), you get back a reference to an object that you must cast to a Cat. Then you need to surround the entire expression with parentheses to force the evaluation of the cast before calling the print( ) method for Cat, otherwise you’ll get a syntax error. Then, at run-time, when you try to cast the Dog object to a Cat, you’ll get an exception.

This is more than just an annoyance. It’s something that can create difficult-to-find bugs. If one part (or several parts) of a program inserts objects into a container, and you discover only in a separate part of the program through an exception that a bad object was placed in the container, then you must find out where the bad insert occurred. On the upside, it’s convenient to start with some standardized container classes for programming, despite the scarcity and awkwardness.

It turns out that in some cases things seem to work correctly without casting back to your original type. One case is quite special: the String class has some extra help from the compiler to make it work smoothly. Whenever the compiler expects a String object and it hasn’t got one, it will automatically call the toString( ) method that’s defined in Object and can be overridden by any Java class. This method produces the desired String object, which is then used wherever it was wanted.

Thus, all you need to do to make objects of your class print is to override the toString( ) method, as shown in the following example:

You can see toString( ) overridden in Mouse. In the second for loop in main( ) you find the statement:

After the ‘+’ sign the compiler expects to see a String object. get( ) produces an Object, so to get the desired String the compiler implicitly calls toString( ). Unfortunately, you can work this kind of magic only with String; it isn’t available for any other type.

A second approach to hiding the cast has been placed inside MouseTrap. The caughtYa( ) method accepts not a Mouse, but an Object, which it then casts to a Mouse. This is quite presumptuous, of course, since by accepting an Object anything could be passed to the method. However, if the cast is incorrect—if you passed the wrong type—you’ll get an exception at run-time. This is not as good as compile-time checking but it’s still robust. Note that in the use of this method:

no cast is necessary.

You might not want to give up on this issue just yet. A more ironclad solution is to create a new class using the ArrayList, such that it will accept only your type and produce only your type:

Here’s a test for the new container:

This is similar to the previous example, except that the new MouseList class has a private member of type ArrayList, and methods just like ArrayList. However, it doesn’t accept and produce generic Objects, only Mouse objects.

Note that if MouseList had instead been inherited from ArrayList, the add(Mouse) method would simply overload the existing add(Object) and there would still be no restriction on what type of objects could be added. Thus, the MouseList becomes a surrogate to the ArrayList, performing some activities before passing on the responsibility (see Thinking in Patterns with Java, downloadable at www.BruceEckel.com).

Because a MouseList will accept only a Mouse, if you say:

you will get an error message at compile-time. This approach, while more tedious from a coding standpoint, will tell you immediately if you’re using a type improperly.

Note that no cast is necessary when using get( )—it’s always a Mouse.

This kind of problem isn’t isolated—there are numerous cases in which you need to create new types based on other types, and in which it is useful to have specific type information at compile-time. This is the concept of a parameterized type. In C++, this is directly supported by the language with templates. It is likely that a future version of Java will support some variation of parameterized types; the current front-runner automatically creates classes similar to MouseList.

In any container class, you must have a way to put things in and a way to get things out. After all, that’s the primary job of a container—to hold things. In the ArrayList, add( ) is the way that you insert objects, and get( ) is one way to get things out. ArrayList is quite flexible—you can select anything at any time, and select multiple elements at once using different indexes.

If you want to start thinking at a higher level, there’s a drawback: you need to know the exact type of the container in order to use it. This might not seem bad at first, but what if you start out using an ArrayList, and later on in your program you discover that because of the way you are using the container it would be much more efficient to use a LinkedList instead? Or suppose you’d like to write a piece of generic code that doesn’t know or care what type of container it’s working with, so that it could be used on different types of containers without rewriting that code?

The concept of an iterator can be used to achieve this abstraction. An iterator is an object whose job is to move through a sequence of objects and select each object in that sequence without the client programmer knowing or caring about the underlying structure of that sequence. In addition, an iterator is usually what’s called a “light-weight” object: one that’s cheap to create. For that reason, you’ll often find seemingly strange constraints for iterators; for example, some iterators can move in only one direction.

The Java Iterator is an example of an iterator with these kinds of constraints. There’s not much you can do with one except:

That’s all. It’s a simple implementation of an iterator, but still powerful (and there’s a more sophisticated ListIterator for Lists). To see how it works, let’s revisit the CatsAndDogs.java program from earlier in this chapter. In the original version, the method get( ) was used to select each element, but in the following modified version an Iterator is used:

You can see that the only change is in the last few lines, where an Iterator is used to step through the sequence instead of a for loop. With the Iterator, you don’t need to worry about the number of elements in the container. That’s taken care of for you by hasNext( ) and next( ).

As another example, consider the creation of a general-purpose printing method:

Look closely at printAll( ). Note that there’s no information about the type of sequence. All you have is an Iterator, and that’s all you need to know about the sequence: that you can get the next object, and that you can know when you’re at the end. This idea of taking a container of objects and passing through it to perform an operation on each one is powerful, and will be seen throughout this book.

The example is even more generic, since it implicitly uses the Object.toString( ) method. The println( ) method is overloaded for all the primitive types as well as Object; in each case a String is automatically produced by calling the appropriate toString( ) method.

Although it’s unnecessary, you can be more explicit using a cast, which has the effect of calling toString( ):

In general, however, you’ll want to do something more than call Object methods, so you’ll run up against the type-casting issue again. You must assume you’ve gotten an Iterator to a sequence of the particular type you’re interested in, and cast the resulting objects to that type (getting a run-time exception if you’re wrong).

Because (like every other class), the Java standard containers are inherited from Object, they contain a toString( ) method. This has been overridden so that they can produce a String representation of themselves, including the objects they hold. Inside ArrayList, for example, the toString( ) steps through the elements of the ArrayList and calls toString( ) for each one. Suppose you’d like to print the address of your class. It seems to make sense to simply refer to this (in particular, C++ programmers are prone to this approach):

If you simply create an InfiniteRecursion object and then print it, you’ll get an endless sequence of exceptions. This is also true if you place the InfiniteRecursion objects in an ArrayList and print that ArrayList as shown here. What’s happening is automatic type conversion for Strings. When you say:

The compiler sees a String followed by a ‘+’ and something that’s not a String, so it tries to convert this to a String. It does this conversion by calling toString( ), which produces a recursive call.

If you really do want to print the address of the object in this case, the solution is to call the Object toString( ) method, which does just that. So instead of saying this, you’d say super.toString( ). (This only works if you're directly inheriting from Object, or if none of your parent classes have overridden the toString( ) method.)

Collections and Maps may be implemented in different ways, according to your programming needs. It’s helpful to look at a diagram of the Java 2 containers:

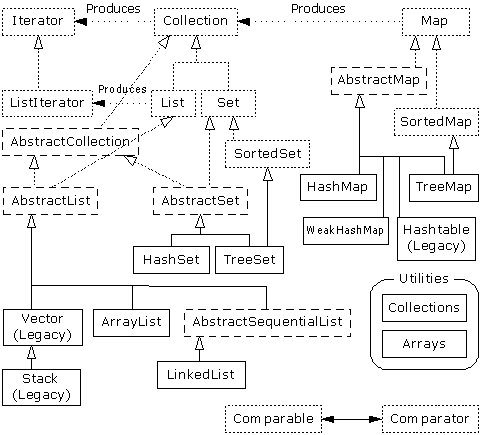
This diagram can be a bit overwhelming at first, but you’ll see that there are really only three container components: Map, List, and Set, and only two or three implementations of each one (with, typically, a preferred version). When you see this, the containers are not so daunting.

The dotted boxes represent interfaces, the dashed boxes represent abstract classes, and the solid boxes are regular (concrete) classes. The dotted-line arrows indicate that a particular class is implementing an interface (or in the case of an abstract class, partially implementing that interface). The solid arrows show that a class can produce objects of the class the arrow is pointing to. For example, any Collection can produce an Iterator, while a List can produce a ListIterator (as well as an ordinary Iterator, since List is inherited from Collection).

The interfaces that are concerned with holding objects are Collection, List, Set, and Map. Ideally, you’ll write most of your code to talk to these interfaces, and the only place where you’ll specify the precise type you’re using is at the point of creation. So you can create a List like this:

Of course, you can also decide to make x a LinkedList (instead of a generic List) and carry the precise type information around with x. The beauty (and the intent) of using the interface is that if you decide you want to change your implementation, all you need to do is change it at the point of creation, like this:

The rest of your code can remain untouched (some of this genericity can also be achieved with iterators).

In the class hierarchy, you can see a number of classes whose names begin with “Abstract,” and these can seem a bit confusing at first. They are simply tools that partially implement a particular interface. If you were making your own Set, for example, you wouldn’t start with the Set interface and implement all the methods, instead you’d inherit from AbstractSet and do the minimal necessary work to make your new class. However, the containers library contains enough functionality to satisfy your needs virtually all the time. So for our purposes, you can ignore any class that begins with “Abstract.”

Therefore, when you look at the diagram, you’re really concerned with only those interfaces at the top of the diagram and the concrete classes (those with solid boxes around them). You’ll typically make an object of a concrete class, upcast it to the corresponding interface, and then use the interface throughout the rest of your code. In addition, you do not need to consider the legacy elements when writing new code. Therefore, the diagram can be greatly simplified to look like this:

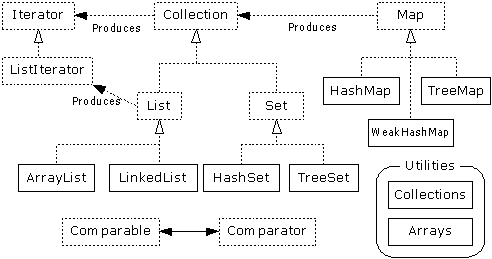
Now it only includes the interfaces and classes that you will encounter on a regular basis, and also the elements that we will focus on in this chapter.

Here’s a simple example, which fills a Collection (represented here with an ArrayList) with String objects, and then prints each element in the Collection:

The first line in main( ) creates an ArrayList object and then upcasts it to a Collection. Since this example uses only the Collection methods, any object of a class inherited from Collection would work, but ArrayList is the typical workhorse Collection.

The add( ) method, as its name suggests, puts a new element in the Collection. However, the documentation carefully states that add( ) “ensures that this Container contains the specified element.” This is to allow for the meaning of Set, which adds the element only if it isn’t already there. With an ArrayList, or any sort of List, add( ) always means “put it in,” because Lists don’t care if there are duplicates.

All Collections can produce an Iterator via their iterator( ) method. Here, an Iterator is created and used to traverse the Collection, printing each element.

The following table shows everything you can do with a Collection (not including the methods that automatically come through with Object), and thus, everything you can do with a Set or a List. (List also has additional functionality.) Maps are not inherited from Collection, and will be treated separately.

Notice that there’s no get( ) function for random-access element selection. That’s because Collection also includes Set, which maintains its own internal ordering (and thus makes random-access lookup meaningless). Thus, if you want to examine all the elements of a Collection you must use an iterator; that’s the only way to fetch things back.

The following example demonstrates all of these methods. Again, these work with anything that inherits from Collection, but an ArrayList is used as a kind of “least-common denominator”:

ArrayLists are created containing different sets of data and upcast to Collection objects, so it’s clear that nothing other than the Collection interface is being used. main( ) uses simple exercises to show all of the methods in Collection.

The following sections describe the various implementations of List, Set, and Map and indicate in each case (with an asterisk) which one should be your default choice. You’ll notice that the legacy classes Vector, Stack, and Hashtable are not included because in all cases there are preferred classes within the Java 2 Containers.

The basic List is quite simple to use, as you’ve seen so far with ArrayList. Although most of the time you’ll just use add( ) to insert objects, get( ) to get them out one at a time, and iterator( ) to get an Iterator to the sequence, there’s also a set of other methods that can be useful.

In addition, there are actually two types of List: the basic ArrayList, which excels at randomly accessing elements, and the much more powerful LinkedList (which is not designed for fast random access, but has a much more general set of methods).

The methods in the following example each cover a different group of activities: things that every list can do (basicTest( )), moving around with an Iterator (iterMotion( )) versus changing things with an Iterator (iterManipulation( )), seeing the effects of List manipulation (testVisual( )), and operations available only to LinkedLists.

In basicTest( ) and iterMotion( ) the calls are simply made to show the proper syntax, and while the return value is captured, it is not used. In some cases, the return value isn’t captured since it isn’t typically used. You should look up the full usage of each of these methods in the online documentation from java.sun.com before you use them.

A stack is sometimes referred to as a “last-in, first-out” (LIFO) container. That is, whatever you “push” on the stack last is the first item you can “pop” out. Like all of the other containers in Java, what you push and pop are Objects, so you must cast what you pop, unless you’re just using Object behavior.

The LinkedList has methods that directly implement stack functionality, so you can also just use a LinkedList rather than making a stack class. However, a stack class can sometimes tell the story better:

If you want only stack behavior, inheritance is inappropriate here because it would produce a class with all the rest of the LinkedList methods (you’ll see later that this very mistake was made by the Java 1.0 library designers with Stack).

A queue is a “first-in, first-out” (FIFO) container. That is, you put things in at one end, and pull them out at the other. So the order in which you put them in will be the same order that they come out. LinkedList has methods to support queue behavior, so these can be used in a Queue class:

You can also easily create a deque (double-ended queue) from a LinkedList. This is like a queue, but you can add and remove elements from either end.

Set has exactly the same interface as Collection, so there isn’t any extra functionality like there is with the two different Lists. Instead, the Set is exactly a Collection, it just has different behavior. (This is the ideal use of inheritance and polymorphism: to express different behavior.) A Set refuses to hold more than one instance of each object value (what constitutes the “value” of an object is more complex, as you shall see).

The following example does not show everything you can do with a Set, since the interface is the same as Collection, and so was exercised in the previous example. Instead, this demonstrates the behavior that makes a Set unique:

Duplicate values are added to the Set, but when it is printed you’ll see the Set has accepted only one instance of each value.

When you run this program you’ll notice that the order maintained by the HashSet is different from TreeSet, since each has a different way of storing elements so they can be located later. (TreeSet keeps them sorted, while HashSet uses a hashing function, which is designed specifically for rapid lookups.) When creating your own types, be aware that a Set needs a way to maintain a storage order, which means you must implement the Comparable interface and define the compareTo( ) method. Here’s an example:

The form for the definitions for equals( ) and hashCode( ) will be described later in this chapter. You must define an equals( ) in both cases, but the hashCode( ) is absolutely necessary only if the class will be placed in a HashSet (which is likely, since that should generally be your first choice as a Set implementation). However, as a programming style you should always override hashCode( ) when you override equals( ). This process will be fully detailed later in this chapter.

In the compareTo( ), note that I did not use the “simple and obvious” form return i-i2. Although this is a common programming error, it would only work properly if i and i2 were “unsigned” ints (if Java had an “unsigned” keyword, which it does not). It breaks for Java’s signed int, which is not big enough to represent the difference of two signed ints. If i is a large positive integer and j is a large negative integer, i-j will overflow and return a negative value, which will not work.

If you have a SortedSet (of which TreeSet is the only one available), the elements are guaranteed to be in sorted order which allows additional functionality to be provided with these methods in the SortedSet interface:

Comparator comparator(): Produces the Comparator used for this Set, or null for natural ordering.

Object first(): Produces the lowest element.

Object last(): Produces the highest element.

SortedSet subSet(fromElement, toElement): Produces a view of this Set with elements from fromElement, inclusive, to toElement, exclusive.

SortedSet headSet(toElement): Produces a view of this Set with elements less than toElement.

SortedSet tailSet(fromElement): Produces a view of this Set with elements greater than or equal to fromElement.

An ArrayList allows you to select from a sequence of objects using a number, so in a sense it associates numbers to objects. But what if you’d like to select from a sequence of objects using some other criterion? A stack is an example: its selection criterion is “the last thing pushed on the stack.” A powerful twist on this idea of “selecting from a sequence” is alternately termed a map, a dictionary, or an associative array. Conceptually, it seems like an ArrayList, but instead of looking up objects using a number, you look them up using another object! This is often a key process in a program.

The concept shows up in Java as the Map interface. The put(Object key, Object value) method adds a value (the thing you want), and associates it with a key (the thing you look it up with). get(Object key) produces the value given the corresponding key. You can also test a Map to see if it contains a key or a value with containsKey( ) and containsValue( ).

The standard Java library contains two different types of Maps: HashMap and TreeMap. Both have the same interface (since they both implement Map), but they differ in one distinct way: efficiency. If you look at what must be done for a get( ), it seems pretty slow to search through (for example) an ArrayList for the key. This is where HashMap speeds things up. Instead of a slow search for the key, it uses a special value called a hash code. The hash code is a way to take some information in the object in question and turn it into a “relatively unique” int for that object. All Java objects can produce a hash code, and hashCode( ) is a method in the root class Object. A HashMap takes the hashCode( ) of the object and uses it to quickly hunt for the key. This results in a dramatic performance improvement[51].

Sometimes you’ll also need to know the details of how hashing works, so we’ll look at that a little later.

The following example uses the Collections2.fill( ) method and the test data sets that were previously defined:

The printKeys( ) and printValues( ) methods are not only useful utilities, they also demonstrate how to produce Collection views of a Map. The keySet( ) method produces a Set backed by the keys in the Map. Similar treatment is given to values( ), which produces a Collection containing all the values in the Map. (Note that keys must be unique, while values may contain duplicates.) Since these Collections are backed by the Map, any changes in a Collection will be reflected in the associated Map.

The rest of the program provides simple examples of each Map operation, and tests each type of Map.

As an example of the use of a HashMap, consider a program to check the randomness of Java’s Math.random( ) method. Ideally, it would produce a perfect distribution of random numbers, but to test this you need to generate a bunch of random numbers and count the ones that fall in the various ranges. A HashMap is perfect for this, since it associates objects with objects (in this case, the value object contains the number produced by Math.random( ) along with the number of times that number appears):

In main( ), each time a random number is generated it is wrapped inside an Integer object so that reference can be used with the HashMap. (You can’t use a primitive with a container, only an object reference.) The containsKey( ) method checks to see if this key is already in the container. (That is, has the number been found already?) If so, the get( ) method produces the associated value for the key, which in this case is a Counter object. The value i inside the counter is incremented to indicate that one more of this particular random number has been found.

If the key has not been found yet, the method put( ) will place a new key-value pair into the HashMap. Since Counter automatically initializes its variable i to one when it’s created, it indicates the first occurrence of this particular random number.

To display the HashMap, it is simply printed. The HashMap toString( ) method moves through all the key-value pairs and calls the toString( ) for each one. The Integer.toString( ) is predefined, and you can see the toString( ) for Counter. The output from one run (with some line breaks added) is:

You might wonder at the necessity of the class Counter, which seems like it doesn’t even have the functionality of the wrapper class Integer. Why not use int or Integer? Well, you can’t use an int because all of the containers can hold only Object references. After seeing containers the wrapper classes might begin to make a little more sense to you, since you can’t put any of the primitive types in containers. However, the only thing you can do with the Java wrappers is to initialize them to a particular value and read that value. That is, there’s no way to change a value once a wrapper object has been created. This makes the Integer wrapper immediately useless to solve our problem, so we’re forced to create a new class that does satisfy the need.

If you have a SortedMap (of which TreeMap is the only one available), the keys are guaranteed to be in sorted order which allows additional functionality to be provided with these methods in the SortedMap interface:

Comparator comparator(): Produces the comparator used for this Map, or null for natural ordering.

Object firstKey(): Produces the lowest key.

Object lastKey(): Produces the highest key.

SortedMap subMap(fromKey, toKey): Produces a view of this Map with keys from fromKey, inclusive, to toKey, exclusive.

SortedMap headMap(toKey): Produces a view of this Map with keys less than toKey.

SortedMap tailMap(fromKey): Produces a view of this Map with keys greater than or equal to fromKey.

In the previous example, a standard library class (Integer) was used as a key for the HashMap. It worked fine as a key, because it has all the necessary wiring to make it work correctly as a key. But a common pitfall occurs with HashMaps when you create your own classes to be used as keys. For example, consider a weather predicting system that matches Groundhog objects to Prediction objects. It seems fairly straightforward—you create the two classes, and use Groundhog as the key and Prediction as the value:

Each Groundhog is given an identity number, so you can look up a Prediction in the HashMap by saying, “Give me the Prediction associated with Groundhog number 3.” The Prediction class contains a boolean that is initialized using Math.random( ), and a toString( ) that interprets the result for you. In main( ), a HashMap is filled with Groundhogs and their associated Predictions. The HashMap is printed so you can see that it has been filled. Then a Groundhog with an identity number of 3 is used as a key to look up the prediction for Groundhog #3 (which you can see must be in the Map).

It seems simple enough, but it doesn’t work. The problem is that Groundhog is inherited from the common root class Object (which is what happens if you don’t specify a base class, thus all classes are ultimately inherited from Object). It is Object’s hashCode( ) method that is used to generate the hash code for each object, and by default it just uses the address of its object. Thus, the first instance of Groundhog(3) does not produce a hash code equal to the hash code for the second instance of Groundhog(3) that we tried to use as a lookup.

You might think that all you need to do is write an appropriate override for hashCode( ). But it still won’t work until you’ve done one more thing: override the equals( ) that is also part of Object. This method is used by the HashMap when trying to determine if your key is equal to any of the keys in the table. Again, the default Object.equals( ) simply compares object addresses, so one Groundhog(3) is not equal to another Groundhog(3).

Thus, to use your own classes as keys in a HashMap, you must override both hashCode( ) and equals( ), as shown in the following solution to the problem above:

Note that this uses the Prediction class from the previous example, so SpringDetector.java must be compiled first or you’ll get a compile-time error when you try to compile SpringDetector2.java.

Groundhog2.hashCode( ) returns the groundhog number as an identifier. In this example, the programmer is responsible for ensuring that no two groundhogs exist with the same ID number. The hashCode( ) is not required to return a unique identifier (something you’ll understand better later in this chapter), but the equals( ) method must be able to strictly determine whether two objects are equivalent.

Even though it appears that the equals( ) method is only checking to see whether the argument is an instance of Groundhog2 (using the instanceof keyword, which is fully explained in Chapter 12), the instanceof actually quietly does a second sanity check, to see if the object is null, since instanceof produces false if the left-hand argument is null. Assuming it’s the correct type and not null, the comparison is based on the actual ghNumbers. This time, when you run the program, you’ll see it produces the correct output.

When creating your own class to use in a HashSet, you must pay attention to the same issues as when it is used as a key in a HashMap.

The above example is only a start toward solving the problem correctly. It shows that if you do not override hashCode( ) and equals( ) for your key, the hashed data structure (HashSet or HashMap) will not be able to deal with your key properly. However, to get a good solution for the problem you need to understand what’s going on inside the hashed data structure.

First, consider the motivation behind hashing: you want to look up an object using another object. But you can accomplish this with a TreeSet or TreeMap, too. It’s also possible to implement your own Map. To do so, the Map.entrySet( ) method must be supplied to produce a set of Map.Entry objects. MPair will be defined as the new type of Map.Entry. In order for it to be placed in a TreeSet it must implement equals( ) and be Comparable:

The following example implements a Map using a pair of ArrayLists:

The put( ) method simply places the keys and values in corresponding ArrayLists. In main( ), a SlowMap is loaded and then printed to show that it works.

This shows that it’s not that hard to produce a new type of Map. But as the name suggests, a SlowMap isn’t very fast, so you probably wouldn’t use it if you had an alternative available. The problem is in the lookup of the key: there is no order so a simple linear search is used, which is the slowest way to look something up.

The whole point of hashing is speed: hashing allows the lookup to happen quickly. Since the bottleneck is in the speed of the key lookup, one of the solutions to the problem could be by keeping the keys sorted and then using Collections.binarySearch( ) to perform the lookup (an exercise at the end of this chapter will walk you through this process).

Hashing goes further by saying that all you want to do is to store the key somewhere so that it can be quickly found. As you’ve seen in this chapter, the fastest structure in which to store a group of elements is an array, so that will used for representing the key information (note carefully that I said “key information,” and not the key itself). Also seen in this chapter was the fact that an array, once allocated, cannot be resized, so we have a problem: we want to be able to store any number of values in the Map, but if the number of keys is fixed by the array size, how can this be?

The answer is that the array will not hold the keys. From the key object, a number will be derived that will index into the array. This number is the hash code, produced by the hashCode( ) method (in computer science parlance, this is the hash function) defined in Object and presumably overridden by your class. To solve the problem of the fixed-size array, more than one key may produce the same index. That is, there may be collisions. Because of this, it doesn’t matter how big the array is because each key object will land somewhere in that array.

So the process of looking up a value starts by computing the hash code and using it to index into the array. If you could guarantee that there were no collisions (which could be possible if you have a fixed number of values) then you’d have a perfect hashing function, but that’s a special case. In all other cases, collisions are handled by external chaining: the array points not directly to a value, but instead to a list of values. These values are searched in a linear fashion using the equals( ) method. Of course, this aspect of the search is much slower, but if the hash function is good there will only be a few values in each slot, at the most. So instead of searching through the entire list, you quickly jump to a slot where you have to compare a few entries to find the value. This is much faster, which is why the HashMap is so quick.

Knowing the basics of hashing, it’s possible to implement a simple hashed Map:

Because the “slots” in a hash table are often referred to as buckets, the array that represents the actual table is called bucket. To promote even distribution, the number of buckets is typically a prime number. Notice that it is an array of LinkedList, which automatically provides for collisions—each new item is simply added to the end of the list.

The return value of put( ) is null or, if the key was already in the list, the old value associated with that key. The return value is result, which is initialized to null, but if a key is discovered in the list then result is assigned to that key.

For both put( ) and get( ), the first thing that happens is that the hashCode( ) is called for the key, and the result is forced to a positive number. Then it is forced to fit into the bucket array using the modulus operator and the size of the array. If that location is null, it means there are no elements that hash to that location, so a new LinkedList is created to hold the object that just did. However, the normal process is to look through the list to see if there are duplicates, and if there are, the old value is put into result and the new value replaces the old. The found flag keeps track of whether an old key-value pair was found and, if not, the new pair is appended to the end of the list.

In get( ), you’ll see very similar code as that contained in put( ), but simpler. The index is calculated into the bucket array, and if a LinkedList exists it is searched for a match.

entrySet( ) must find and traverse all the lists, adding them to the result Set. Once this method has been created, the Map can be tested by filling it with values and then printing them.

To understand the issues, some terminology is necessary:

Capacity: The number of buckets in the table.

Initial capacity: The number of buckets when the table is created. HashMap and HashSet: have constructors that allow you to specify the initial capacity.

Size: The number of entries currently in the table.

Load factor: size/capacity. A load factor of 0 is an empty table, 0.5 is a half-full table, etc. A lightly-loaded table will have few collisions and so is optimal for insertions and lookups (but will slow down the process of traversing with an iterator). HashMap and HashSet have constructors that allow you to specify the load factor, which means that when this load factor is reached the container will automatically increase the capacity (the number of buckets) by roughly doubling it, and will redistribute the existing objects into the new set of buckets (this is called rehashing).

The default load factor used by HashMap is 0.75 (it doesn’t rehash until the table is ¾ full). This seems to be a good trade-off between time and space costs. A higher load factor decreases the space required by the table but increases the lookup cost, which is important because lookup is what you do most of the time (including both get( ) and put( )).

If you know that you’ll be storing many entries in a HashMap, creating it with an appropriately large initial capacity will prevent the overhead of automatic rehashing.

Now that you understand what’s involved in the function of the HashMap, the issues involved in writing a hashCode( ) will make more sense.

First of all, you don’t have control of the creation of the actual value that’s used to index into the array of buckets. That is dependent on the capacity of the particular HashMap object, and that capacity changes depending on how full the container is, and what the load factor is. The value produced by your hashCode( ) will be further processed in order to create the bucket index (in SimpleHashMap the calculation is just a modulo by the size of the bucket array).

The most important factor in creating a hashCode( ) is that, regardless of when hashCode( ) is called, it produces the same value for a particular object every time it is called. If you end up with an object that produces one hashCode( ) value when it is put( ) into a HashMap, and another during a get( ), you won’t be able to retrieve the objects. So if your hashCode( ) depends on mutable data in the object the user must be made aware that changing the data will effectively produce a different key by generating a different hashCode( ).

In addition, you will probably not want to generate a hashCode( ) that is based on unique object information—in particular, the value of this makes a bad hashCode( ) because then you can’t generate a new identical key to the one used to put( ) the original key-value pair. This was the problem that occurred in SpringDetector.java because the default implementation of hashCode( ) does use the object address. So you’ll want to use information in the object that identifies the object in a meaningful way.

One example is found in the String class. Strings have the special characteristic that if a program has several String objects that contain identical character sequences, then those String objects all map to the same memory (the mechanism for this is described in Appendix A). So it makes sense that the hashCode( ) produced by two separate instances of new String(“hello”) should be identical. You can see it by running this program:

For this to work, the hashCode( ) for String must be based on the contents of the String.

So for a hashCode( ) to be effective, it must be fast and it must be meaningful: that is, it must generate a value based on the contents of the object. Remember that this value doesn’t have to be unique—you should lean toward speed rather than uniqueness—but between hashCode( ) and equals( ) the identity of the object must be completely resolved.

Because the hashCode( ) is further processed before the bucket index is produced, the range of values is not important; it just needs to generate an int.

There’s one other factor: a good hashCode( ) should result in an even distribution of values. If the values tend to cluster, then the HashMap or HashSet will be more heavily loaded in some areas and will not be as fast as it could be with an evenly distributed hashing function.

Here’s an example that follows these guidelines:

CountedString includes a String and an id that represents the number of CountedString objects that contain an identical String. The counting is accomplished in the constructor by iterating through the static ArrayList where all the Strings are stored.

Both hashCode( ) and equals( ) produce results based on both fields; if they were just based on the String alone or the id alone there would be duplicate matches for distinct values.

Note how simple the hashCode( ) is: String’s hashCode( ) is multiplied by the id. Smaller is generally better (and faster) for hashCode( ).

In main( ), a bunch of CountedString objects are created, using the same String to show that the duplicates create unique values because of the count id.

The java.lang.ref library contains a set of classes that allow greater flexibility in garbage collection, which are especially useful when you have large objects that may cause memory exhaustion. There are three classes inherited from the abstract class Reference: SoftReference, WeakReference, and PhantomReference. Each of these provides a different level of indirection for the garbage collector, if the object in question is only reachable through one of these Reference objects.

If an object is reachable it means that somewhere in your program the object can be found. This could mean that you have an ordinary reference on the stack that goes right to the object, but you might also have a reference to an object that has a reference to the object in question; there could be many intermediate links. If an object is reachable, the garbage collector cannot release it because it’s still in use by your program. If an object isn’t reachable, there’s no way for your program to use it so it’s safe to garbage-collect that object.

You use Reference objects when you want to continue to hold onto a reference to that object—you want to be able to reach that object—but you also want to allow the garbage collector to release that object. Thus, you have a way to go on using the object, but if memory exhaustion is imminent you allow that object to be released.

You accomplish this by using a Reference object as an intermediary between you and the ordinary reference, and there must be no ordinary references to the object (ones that are not wrapped inside Reference objects). If the garbage collector discovers that an object is reachable through an ordinary reference, it will not release that object.

In the order SoftReference, WeakReference, and PhantomReference, each one is “weaker” than the last, and corresponds to a different level of reachability. Soft references are for implementing memory-sensitive caches. Weak references are for implementing “canonicalizing mappings”—where instances of objects can be simultaneously used in multiple places in a program, to save storage—that do not prevent their keys (or values) from being reclaimed. Phantom references are for scheduling pre-mortem cleanup actions in a more flexible way than is possible with the Java finalization mechanism.

With SoftReferences and WeakReferences, you have a choice about whether to place them on a ReferenceQueue (the device used for premortem cleanup actions), but a PhantomReference can only be built on a ReferenceQueue. Here’s a simple demonstration:

When you run this program (you’ll want to pipe the output through a “more” utility so that you can view the output in pages), you’ll see that the objects are garbage-collected, even though you still have access to them through the Reference object (to get the actual object reference, you use get( )). You’ll also see that the ReferenceQueue always produces a Reference containing a null object. To make use of this, you can inherit from the particular Reference class you’re interested in and add more useful methods to the new type of Reference.

The containers library has a special Map to hold weak references: the WeakHashMap. This class is designed to make the creation of canonicalized mappings easier. In such a mapping, you are saving storage by making only one instance of a particular value. When the program needs that value, it looks up the existing object in the mapping and uses that (rather than creating one from scratch). The mapping may make the values as part of its initialization, but it’s more likely that the values are made on demand.

Since this is a storage-saving technique, it’s very convenient that the WeakHashMap allows the garbage collector to automatically clean up the keys and values. You don’t have to do anything special to the keys and values you want to place in the WeakHashMap; these are automatically wrapped in WeakReferences by the map. The trigger to allow cleanup is if the key is no longer in use, as demonstrated here:

The Key class must have a hashCode( ) and an equals( ) since it is being used as a key in a hashed data structure, as described previously in this chapter.

When you run the program you’ll see that the garbage collector will skip every third key, because an ordinary reference to that key has also been placed in the keys array and thus those objects cannot be garbage-collected.

We can now demonstrate the true power of the Iterator: the ability to separate the operation of traversing a sequence from the underlying structure of that sequence. In the following example, the class PrintData uses an Iterator to move through a sequence and call the toString( ) method for every object. Two different types of containers are created—an ArrayList and a HashMap—and they are each filled with, respectively, Mouse and Hamster objects. (These classes are defined earlier in this chapter.) Because an Iterator hides the structure of the underlying container, PrintData doesn’t know or care what kind of container the Iterator comes from:

For the HashMap, the entrySet( ) method produces a Set of Map.entry objects, which contain both the key and the value for each entry, so you see both of them printed.

Note that PrintData.print( ) takes advantage of the fact that the objects in these containers are of class Object so the call toString( ) by System.out.println( ) is automatic. It’s more likely that in your problem, you must make the assumption that your Iterator is walking through a container of some specific type. For example, you might assume that everything in the container is a Shape with a draw( ) method. Then you must downcast from the Object that Iterator.next( ) returns to produce a Shape.

By now you should understand that there are really only three container components: Map, List, and Set, and only two or three implementations of each interface. If you need to use the functionality offered by a particular interface, how do you decide which particular implementation to use?

To understand the answer, you must be aware that each different implementation has its own features, strengths, and weaknesses. For example, you can see in the diagram that the “feature” of Hashtable, Vector, and Stack is that they are legacy classes, so that old code doesn’t break. On the other hand, it’s best if you don’t use those for new (Java 2) code.

The distinction between the other containers often comes down to what they are “backed by”; that is, the data structures that physically implement your desired interface. This means that, for example, ArrayList and LinkedList implement the List interface so your program will produce the same results regardless of the one you use. However, ArrayList is backed by an array, while the LinkedList is implemented in the usual way for a doubly linked list, as individual objects each containing data along with references to the previous and next elements in the list. Because of this, if you want to do many insertions and removals in the middle of a list, a LinkedList is the appropriate choice. (LinkedList also has additional functionality that is established in AbstractSequentialList.) If not, an ArrayList is typically faster.

As another example, a Set can be implemented as either a TreeSet or a HashSet. A TreeSet is backed by a TreeMap and is designed to produce a constantly sorted set. However, if you’re going to have larger quantities in your Set, the performance of TreeSet insertions will get slow. When you’re writing a program that needs a Set, you should choose HashSet by default, and change to TreeSet when it's more important to have a constantly sorted set.

The most convincing way to see the differences between the implementations of List is with a performance test. The following code establishes an inner base class to use as a test framework, then creates an array of anonymous inner classes, one for each different test. Each of these inner classes is called by the test( ) method. This approach allows you to easily add and remove new kinds of tests.

The inner class Tester is abstract, to provide a base class for the specific tests. It contains a String to be printed when the test starts, a size parameter to be used by the test for quantity of elements or repetitions of tests, a constructor to initialize the fields, and an abstract method test( ) that does the work. All the different types of tests are collected in one place, the array tests, which is initialized with different anonymous inner classes that inherit from Tester. To add or remove tests, simply add or remove an inner class definition from the array, and everything else happens automatically.

To compare array access to container access (primarily against ArrayList), a special test is created for arrays by wrapping one as a List using Arrays.asList( ). Note that only the first two tests can be performed in this case, because you cannot insert or remove elements from an array.

The List that’s handed to test( ) is first filled with elements, then each test in the tests array is timed. The results will vary from machine to machine; they are intended to give only an order of magnitude comparison between the performance of the different containers. Here is a summary of one run:

As expected, arrays are faster than any container for random-access lookups and iteration. You can see that random accesses (get( )) are cheap for ArrayLists and expensive for LinkedLists. (Oddly, iteration is faster for a LinkedList than an ArrayList, which is a bit counterintuitive.) On the other hand, insertions and removals from the middle of a list are dramatically cheaper for a LinkedList than for an ArrayList—especially removals. Vector is generally not as fast as ArrayList, and it should be avoided; it’s only in the library for legacy code support (the only reason it works in this program is because it was adapted to be a List in Java 2). The best approach is probably to choose an ArrayList as your default, and to change to a LinkedList if you discover performance problems due to many insertions and removals from the middle of the list. And of course, if you are working with a fixed-sized group of elements, use an array.

You can choose between a TreeSet and a HashSet, depending on the size of the Set (if you need to produce an ordered sequence from a Set, use TreeSet). The following test program gives an indication of this trade-off:

The following table shows the results of one run. (Of course, this will be different according to the computer and JVM you are using; you should run the test yourself as well):

The performance of HashSet is generally superior to TreeSet for all operations (but in particular addition and lookup, the two most important operations). The only reason TreeSet exists is because it maintains its elements in sorted order, so you only use it when you need a sorted Set.

When choosing between implementations of Map, the size of the Map is what most strongly affects performance, and the following test program gives an indication of this trade-off:

Because the size of the map is the issue, you’ll see that the timing tests divide the time by the size to normalize each measurement. Here is one set of results. (Yours will probably be different.)

As you might expect, Hashtable performance is roughly equivalent to HashMap. (You can also see that HashMap is generally a bit faster. HashMap is intended to replace Hashtable.) The TreeMap is generally slower than the HashMap, so why would you use it? So you could use it not as a Map, but as a way to create an ordered list. The behavior of a tree is such that it’s always in order and doesn’t have to be specially sorted. Once you fill a TreeMap, you can call keySet( ) to get a Set view of the keys, then toArray( ) to produce an array of those keys. You can then use the static method Arrays.binarySearch( ) (discussed later) to rapidly find objects in your sorted array. Of course, you would probably only do this if, for some reason, the behavior of a HashMap was unacceptable, since HashMap is designed to rapidly find things. Also, you can easily create a HashMap from a TreeMap with a single object creation In the end, when you’re using a Map your first choice should be HashMap, and only if you need a constantly sorted Map will you need TreeMap.

Utilities to perform sorting and searching for Lists have the same names and signatures as those for sorting arrays of objects, but are static methods of Collections instead of Arrays. Here’s an example, modified from ArraySearching.java:

The use of these methods is identical to the ones in Arrays, but you’re using a List instead of an array. Just like searching and sorting with arrays, if you sort using a Comparator you must binarySearch( ) using the same Comparator.

This program also demonstrates the shuffle( ) method in Collections, which randomizes the order of a List.

There are a number of other useful utilities in the Collections class:

Note that min( ) and max( ) work with Collection objects, not with Lists, so you don’t need to worry about whether the Collection should be sorted or not. (As mentioned earlier, you do need to sort( ) a List or an array before performing a binarySearch( ).)

Often it is convenient to create a read-only version of a Collection or Map. The Collections class allows you to do this by passing the original container into a method that hands back a read-only version. There are four variations on this method, one each for Collection (if you don’t want to treat a Collection as a more specific type), List, Set, and Map. This example shows the proper way to build read-only versions of each:

In each case, you must fill the container with meaningful data before you make it read-only. Once it is loaded, the best approach is to replace the existing reference with the reference that is produced by the “unmodifiable” call. That way, you don’t run the risk of accidentally changing the contents once you’ve made it unmodifiable. On the other hand, this tool also allows you to keep a modifiable container as private within a class and to return a read-only reference to that container from a method call. So you can change it from within the class, but everyone else can only read it.

Calling the “unmodifiable” method for a particular type does not cause compile-time checking, but once the transformation has occurred, any calls to methods that modify the contents of a particular container will produce an UnsupportedOperationException.

The synchronized keyword is an important part of the subject of multithreading, a more complicated topic that will not be introduced until Chapter 14. Here, I shall note only that the Collections class contains a way to automatically synchronize an entire container. The syntax is similar to the “unmodifiable” methods:

In this case, you immediately pass the new container through the appropriate “synchronized” method; that way there’s no chance of accidentally exposing the unsynchronized version.

The Java containers also have a mechanism to prevent more than one process from modifying the contents of a container. The problem occurs if you’re iterating through a container and some other process steps in and inserts, removes, or changes an object in that container. Maybe you’ve already passed that object, maybe it’s ahead of you, maybe the size of the container shrinks after you call size( )—there are many scenarios for disaster. The Java containers library incorporates a fail-fast mechanism that looks for any changes to the container other than the ones your process is personally responsible for. If it detects that someone else is modifying the container, it immediately produces a ConcurrentModificationException. This is the “fail-fast” aspect—it doesn’t try to detect a problem later on using a more complex algorithm.

It’s possible to turn an array into a List with the Arrays.asList( ) method:

You’ll discover that only a portion of the Collection and List interfaces are actually implemented. The rest of the methods cause the unwelcome appearance of something called an UnsupportedOperationException. You’ll learn all about exceptions in the next chapter, but the short story is that the Collection interface—as well as some of the other interfaces in the Java containers library—contain “optional” methods, which might or might not be “supported” in the concrete class that implements that interface. Calling an unsupported method causes an UnsupportedOperationException to indicate a programming error.

“What?!?” you say, incredulous. “The whole point of interfaces and base classes is that they promise these methods will do something meaningful! This breaks that promise—it says that not only will calling some methods not perform a meaningful behavior, they will stop the program! Type safety was just thrown out the window!”

It’s not quite that bad. With a Collection, List, Set, or Map, the compiler still restricts you to calling only the methods in that interface, so it’s not like Smalltalk (in which you can call any method for any object, and find out only when you run the program whether your call does anything). In addition, most methods that take a Collection as an argument only read from that Collection—all the “read” methods of Collection are not optional.

This approach prevents an explosion of interfaces in the design. Other designs for container libraries always seem to end up with a confusing plethora of interfaces to describe each of the variations on the main theme and are thus difficult to learn. It’s not even possible to capture all of the special cases in interfaces, because someone can always invent a new interface. The “unsupported operation” approach achieves an important goal of the Java containers library: the containers are simple to learn and use; unsupported operations are a special case that can be learned later. For this approach to work, however:

In the example above, Arrays.asList( ) produces a List that is backed by a fixed-size array. Therefore it makes sense that the only supported operations are the ones that don’t change the size of the array. If, on the other hand, a new interface were required to express this different kind of behavior (called, perhaps, “FixedSizeList”), it would throw open the door to complexity and soon you wouldn’t know where to start when trying to use the library.

The documentation for a method that takes a Collection, List, Set, or Map as an argument should specify which of the optional methods must be implemented. For example, sorting requires the set( ) and Iterator.set( ) methods, but not add( ) and remove( ).

Unfortunately, a lot of code was written using the Java 1.0/1.1 containers, and even new code is sometimes written using these classes. So although you should never use the old containers when writing new code, you’ll still need to be aware of them. However, the old containers were quite limited, so there’s not that much to say about them. (Since they are in the past, I will try to refrain from overemphasizing some of the hideous design decisions.)

The only self-expanding sequence in Java 1.0/1.1 was the Vector, and so it saw a lot of use. Its flaws are too numerous to describe here (see the first edition of this book, available on this book’s CD ROM and as a free download from www.BruceEckel.com). Basically, you can think of it as an ArrayList with long, awkward method names. In the Java 2 container library, Vector was adapted so that it could fit as a Collection and a List, so in the following example the Collections2.fill( ) method is successfully used. This turns out to be a bit perverse, as it may confuse some people into thinking that Vector has gotten better, when it is actually included only to support pre-Java 2 code.

The Java 1.0/1.1 version of the iterator chose to invent a new name, “enumeration,” instead of using a term that everyone was already familiar with. The Enumeration interface is smaller than Iterator, with only two methods, and it uses longer method names: boolean hasMoreElements( ) produces true if this enumeration contains more elements, and Object nextElement( ) returns the next element of this enumeration if there are any more (otherwise it throws an exception).

Enumeration is only an interface, not an implementation, and even new libraries sometimes still use the old Enumeration—which is unfortunate but generally harmless. Even though you should always use Iterator when you can in your own code, you must be prepared for libraries that want to hand you an Enumeration.

In addition, you can produce an Enumeration for any Collection by using the Collections.enumeration( ) method, as seen in this example:

The Java 1.0/1.1 Vector has only an addElement( ) method, but fill( ) uses the add( ) method that was pasted on as Vector was turned into a List. To produce an Enumeration, you call elements( ), then you can use it to perform a forward iteration.

The last line creates an ArrayList and uses enumeration( ) to adapt an Enumeration from the ArrayList Iterator. Thus, if you have old code that wants an Enumeration, you can still use the new containers.

As you’ve seen in the performance comparison in this chapter, the basic Hashtable is very similar to the HashMap, even down to the method names. There’s no reason to use Hashtable instead of HashMap in new code.

The concept of the stack was introduced earlier, with the LinkedList. What’s rather odd about the Java 1.0/1.1 Stack is that instead of using a Vector as a building block, Stack is inherited from Vector. So it has all of the characteristics and behaviors of a Vector plus some extra Stack behaviors. It’s difficult to know whether the designers explicitly decided that this was an especially useful way of doing things, or whether it was just a naive design.

Here’s a simple demonstration of Stack that pushes each line from a String array:

Each line in the months array is inserted into the Stack with push( ), and later fetched from the top of the stack with a pop( ). To make a point, Vector operations are also performed on the Stack object. This is possible because, by virtue of inheritance, a Stack is a Vector. Thus, all operations that can be performed on a Vector can also be performed on a Stack, such as elementAt( ).

As mentioned earlier, you should use a LinkedList when you want stack behavior.

A BitSet is used if you want to efficiently store a lot of on-off information. It’s efficient only from the standpoint of size; if you’re looking for efficient access, it is slightly slower than using an array of some native type.

In addition, the minimum size of the BitSet is that of a long: 64 bits. This implies that if you’re storing anything smaller, like 8 bits, a BitSet will be wasteful; you’re better off creating your own class, or just an array, to hold your flags if size is an issue.

A normal container expands as you add more elements, and the BitSet does this as well. The following example shows how the BitSet works:

The random number generator is used to create a random byte, short, and int, and each one is transformed into a corresponding bit pattern in a BitSet. This works fine because a BitSet is 64 bits, so none of these cause it to increase in size. Then a BitSet of 512 bits is created. The constructor allocates storage for twice that number of bits. However, you can still set bit 1024 or greater.

To review the containers provided in the standard Java library:

The containers are tools that you can use on a day-to-day basis to make your programs simpler, more powerful, and more effective.

[45] It’s possible, however, to ask how big the vector is, and the at( ) method does perform bounds checking.

[46] This is one of the places where C++ is distinctly superior to Java, since C++ supports parameterized types with the template keyword.

[47] The C++ programmer will note how much the code could be collapsed with the use of default arguments and templates. The Python programmer will note that this entire library would be largely unnecessary in that language.

[48] By Joshua Bloch at Sun.

[49] This data was found on the Internet, then processed by creating a Python program (see www.Python.org).

[50] This is a place where operator overloading would be nice.

[51] If these speedups still don’t meet your performance needs, you can further accelerate table lookup by writing your own Map and customizing it to your particular types to avoid delays due to casting to and from Objects. To reach even higher levels of performance, speed enthusiasts can use Donald Knuth’s The Art of Computer Programming, Volume 3: Sorting and Searching, Second Edition to replace overflow bucket lists with arrays that have two additional benefits: they can be optimized for disk storage characteristics and they can save most of the time of creating and garbage collecting individual records.