



Next: Sequent Calculus
Up: Chaining Inferences
Previous: Selection Functions.
Contents
Restrictions for Inferences.
Given an ordering and a selection function,
the chaining inferences are restricted
in that an inference is performed only between maximal or selected
atoms in a clause, and only if the middle term through which
is being chained is maximal (with respect to the given reduction
ordering 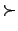 ) in both atoms:
) in both atoms:
-
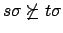 ,
,
-
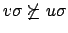 ,
,
- the participating
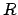 -atoms must either be maximal or
selected within the repsective premises; and
-atoms must either be maximal or
selected within the repsective premises; and
- the positive (that is, first) premise of an inference
contains no selected literals.
Hence, selection not only indicates which subgoal to solve
in a clause. It also serves to block clauses from
becoming a positive premise in an inference.
Unrestricted chaining amounts to hyperresolution
with the transitivity axiom and creates a large search space.
This is illustrated by the two examples HRES15
and OC15
which both consist of
the facts 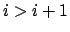 , for
, for 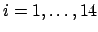 , together with the transitivity axiom
for
, together with the transitivity axiom
for 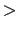 . In the case of HRES15, the ordering restrictions are turned
off. To saturate HRES15 takes about 100 times longer than
running the example in the unsual ordered chaining mode OC15.
. In the case of HRES15, the ordering restrictions are turned
off. To saturate HRES15 takes about 100 times longer than
running the example in the unsual ordered chaining mode OC15.




Next: Sequent Calculus
Up: Chaining Inferences
Previous: Selection Functions.
Contents
Harald Ganzinger
2002-12-04
Imprint | Data Protection
![]() , for
, for ![]() , together with the transitivity axiom
for
, together with the transitivity axiom
for ![]() . In the case of HRES15, the ordering restrictions are turned
off. To saturate HRES15 takes about 100 times longer than
running the example in the unsual ordered chaining mode OC15.
. In the case of HRES15, the ordering restrictions are turned
off. To saturate HRES15 takes about 100 times longer than
running the example in the unsual ordered chaining mode OC15.