Chaining Inferences

Transitivity of a relation $R$, say, is dealt with by chaining inferences of the form

$$\strut\displaystyle {C, R(s,t) \quad\quad D, R(u,v)} \over \strut\displaystyle {(C, D, R(s,v))\rho}$$

with $\rho$ the mgu of $t$ and $u$. Its dual, negative chaining, is an inference of the form

$$\strut C , R(t,s) \quad D , \neg R(u,v) \over \strut ( C , D , \neg R(s,v) )\rho$$

or

$$\strut C , R(s,t) \quad D , \neg R(v,u) \over \strut ( C , D , \neg R(v,s) )\rho$$

with $\rho$ the mgu of $t$ and $u$.

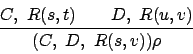
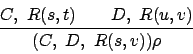
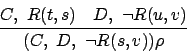
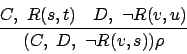
As can be seen, paramodulation is a special case of chaining. In fact, equality is a binary relation for which we have transitivity, reflexivity, symmetry and monotonicity for all function and predicate symbols. Monotonicity or anti-monotonicity axioms can be dealt with by chaining into subterms. At present, subterm chaining is only implemented for partial congruences including equality. Resolution, too, is a special case of negative chaining

$$\strut C , A\mathrel{\mbox{{\tt ==}}}\top \quad D , \neg ... ...C\sigma , D\sigma , \neg (\top\mathrel{\mbox{{\tt ==}}}\top)$$

between two equivalences $A\mathrel{\mbox{{\tt ==}}}\top$ and $B\mathrel{\mbox{{\tt ==}}}\top$ with subsequent deletion of the trivial equation $\top\mathrel{\mbox{{\tt ==}}}\top$, where $\rho$ is the mgu of $A$ and $B$.

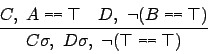
Saturate attempts to automatically recognize relevant properties of binary relations, including transitivity, in order to find an appropriate tailoring of the chaining inference system.

The chaining inference system in Saturate is parameterized by essentially two meta-logical parameters: orderings and selection function. Ordering and selection function induce essential restrictions that one may place on inferences without compromising refutational completeness.

Imprint | Data Protection