



Next: Selection Functions.
Up: Chaining Inferences
Previous: Chaining Inferences
Contents
Reduction Orderings.
When we speak of an ordering we mean a total (or completable)
reduction ordering. A reduction ordering is a well-founded ordering on ground terms
that is compatible with contexts and is total or can be extended to
a total such ordering.
Reduction orderings are the basis for terminating computations
by term rewriting. Saturate provides several classes of reduction
orderings, including the lexicographic path ordering
and its AC-variant.
Orderings specify an orientation of binary atoms, in particular equalities,
indicating the preferred direction when replacing equals by equals.
A ordering 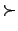 also expresses preferences and directions
of search when attempting to construct models
for disjunctions:
also expresses preferences and directions
of search when attempting to construct models
for disjunctions: 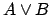 is to be viewed as
is to be viewed as 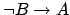 , if
, if 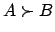 ,
and this links ordered resolution to negation as failure in logic programming.
,
and this links ordered resolution to negation as failure in logic programming.
Harald Ganzinger
2002-12-04
Imprint | Data Protection