sarp: Selecting Redundancy Proof Techniques

$$\mbox{{\tt sarp}}$$

specifies the set of techniques for Redundancy Proofs and for simplification.

These methods are currently implemented and associated with these options $P$:

$P=1$:

tautology elimination

$P=2$:

forward subsumption

$P=3$:

backward subsumption

$P=4$:

condensement

$P=5$:

propositional reasoning for ground clauses

$P=6$:

forward simplification by reduction

$P=7$:

backward simplification by reduction

$P=8$:

redundancy tests by case analysis (forward)

$P=9$:

redundancy tests by case analysis (backward)

$P=10$:

redundancy tests by clausal rewriting (forward)

$P=12$:

totality resolution

$P=13$:

extensionality resolution

$P=14$:

minimal level of reduction

$P=15$:

maximal level of reduction

If $P=15$ is set, reduction is recursive rewriting of ``maximal strength'' where most clauses and their contrapositives are considered as conditional rewrite rules. Reduction also includes convergence tests for inequalities in clauses with respect to the current set of positive unit inequalities. This setting can be very expensive. With $P=14$, only unit clauses are used for reduction which usually is much faster. If neither option is present, an intermediate level of reduction strength is assumed (default setting).

Subsumption always includes a particular form of contextual reduction, also called resolution subsumption. Consider a resolution inference

$$\strut C,A \quad D,B \over \strut D$$

in the case when $A\sigma = \neg B$ and $C\sigma\subseteq D$. Here the conclusion subsumes the second premise which can then be deleted. As to whether such an inference is possible is detected by a subsumption-like algorithm. This is why it has been included into subsumption so as to not duplicate work. Reductions of this form are extremely useful in many examples.

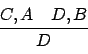
Propositional reasoning for ground clauses refers to an integration of an incremental Davis-Putnam-like procedure for testing satisfiablity of propositional clauses contributed by Peter Barth. The procedure is part of his CLP(PB)-system and is operational only in the SICStus 3.0 version of SaturateRefutational completeness with this method switched on is guaranteed only for ordered strategies without selection as invoked through saci([]).

Totality resolution eliminates, in the case of total relations $p$, all negative occurrences of $p$ by swapping them to the other side of the sequent. This option, by contrast to using the totality axiom lazily, is generally recommended for total orderings, in particular when combined with a positive strategy (sass([2])).

Extensionality resolution is a simplification related to the presence of an extensionality axiom for equality or some other transitive relation. It is somewhat experimental in nature.

Case analysis and clausal rewriting are described in more detail in paper by Nivela and Nieuwenhuis. Case analysis is useful for theories with AC-operators that are to be dealt with by ordered rewriting with option(ac(off)). Clausal rewriting should be turned on for non-trivial consistent theories that one wants to saturate finitely. For refutational theorem proving it should be turned off as it is very expensive.

Imprint | Data Protection