Deduction at Scale 2011
The motivation for the 2011 seminar topic is to get a focus on work for scaling deduction tools and problems. Several deduction communities including the automated and interactive theorem proving community, the SAT and SMT community, the model checking community, the DL community to name at least some, are nowadays challenged by increasingly large problems arising from real world applications. We want to bring together leading researchers from those communities sharing their solutions and challenges.
In addition to giving a talk on "Deduction at Scale" we encourage all participants to bring, present and share challenge problems, being it problems you would like seeing solved or you are proud of having solved.
Venue
The seminar will take place at Ringberg Castle, Tegernsee, Germany. The castle is owned by the Max Planck Society.
For futher information please visit the website of Ringberg Castle.

Program
Participants
| Franz Baader, TU Dresden |
Scaling up by scaling down, or: Small is Again Beautiful in Description Logics Description Logics (DLs) are a popular family of logic-based
knowledge representation languages, which have been used
in various application domains such as natural language
processing, databases, configuration of technical systems,
biomedical ontologies, and the Semantic Web. The Description
Logic (DL) research of the last 20 years was mainly concerned
with increasing the expressive power of the employed
description language without losing the ability of implementing
highly-optimized reasoning systems that behave well in practice,
in spite of the ever increasing worst-case complexity of the underlying
inference problems. |
| Armin Biere, Johannes Kepler University Linz |
Unhiding Redundancy in SAT Preprocessing and inprocessing is used in state-of-the-art SAT solvers to remove redundancy in CNFs. In order to scale these techniques to large instances we recently focused on binary implication graphs. In this talk we revisit these techniques and present a new approach to effectively and efficiently remove redundant clauses and literals. |
| Nikolaij Bjorner, Microsoft Research |
Scaling SMT Solving for Applications Z3 is an efficient Satisfiability Modulo Theories (SMT) solver freely available from Microsoft Research. It is used in several research projects, both within Microsoft Research and in academic research laboratories, and it is used in production for analyzing drivers in the Static Driver Verifier tool and in the SAGE smart white-box fuzzing tool. We take a perspective on Z3 from the point of view of how applications drive the tool. While applications maintain common themes of posing predominantly quantifier-free queries over a set of base theories of un-interpreted functions, arithmetic and bit-vectors, their requirements regarding scale vary significantly. The Pex tool based on dynamic symbolic execution poses many smaller queries to Z3 and includes a precise encoding of the .NET type system, while the related SAGE tool for x86 binary analysis poses larger queries over mostly bit-vectors. The VCC (Verifying C Compiler) tool poses queries combining arrays, quantifiers and integer arithmetic resulting in queries with 100K+ terms, a few thousand clauses, a few hundred integer variables. Other applications, such as the model-based software development tool FORMULA, produce queries that mix algebraic data-types, mixed-integer arithmetic and bit-vectors, in an environment where constraint solving is used for symbolic execution. |
| Jasmin Christian Blanchette, TU München |
Sledgehammer Hell: The Day after Judgment Sledgehammer is a component of Isabelle/HOL that employs resolution provers and SMT solvers to discharge goals arising in interactive proofs. The problems generated by Sledgehammer are unfriendly in many ways: They include hundreds of axioms (corresponding to HOL definitions and theorems), large terms, and lots of type information. In this talk, I will present empirical data to expose the main scalability issues in Sledgehammer, suggesting directions for future research. |
| Sascha Böhme, TU München |
Low-level code and high-level theorems C code is undoubtly low-level, and consequently, verification of C code is mostly concerned with low-level arguments. Yet, full functional verification of C code might also require sophisticated mathematical theorems, typically expressed at a high level of abstraction. We describe the combination of a C code verifier and an interactive theorem prover for functional verification of C code, leaving low-level reasoning to the code verifier and resorting to the interactive theorem prover for high-level theorems -- without exposing each to the other's intricacies. |
| Adnan Darwiche, University of California |
Logic and Probability: The Computational Connection I will discuss in this talk the subject of knowledge compilation of propositional knowledge bases and how it can form the basis for building state-of-the-art probabilistic reasoning systems. In the first part of the talk, I will focus on exact probabilistic reasoning and how it can be reduced to knowledge compilation, leading to an award-winning system for exact inference in the presence of local structure (determinism and context specific independence). In the second part of the talk, I will focus on approximate inference, and how it can be formulated in terms of "relaxing" logical constraints (equalities in particular) for the purpose of aiding the process of knowledge compilation. The resulting formulation, known as "Relax, Compensate and then Recover," subsumes loopy belief propagation and some of its generalizations, and is the basis for an award-winning system at the UAI inference competition in 2010. I will also review in the talk some recent advances and ongoing work in the world of knowledge compilation and the impact it has on the state-of-the-art in probabilistic and symbolic reasoning. |
| Leonardo de Moura, Microsoft Research |
Universal-Z3: A Model Finder for Quantified SMT Formulas Universal-Z3 is a new model finder for quantified SMT formulas. It is implemented on top of the Z3 SMT engine. The core of Universal-Z3 is a counter-example based refinement loop, where candidate models are built and checked. When the model checking step fails, it creates new quantifier instantiations. The models are returned as simple functional programs. Universal-Z3 is also a decision procedure for many known decidable fragments such as: EPR (Effectively Propositional), Bradley&Manna&Sipma's array fragment, Almost Uninterpreted Fragment, McPeak&Necula's list fragment, QBVF (Quantified Bit-Vector Formulas), to cite a few. Universal-Z3 is useful for checking the consistency of background axiomatizations, synthesizing functions, and building real counterexamples for verification tools. Users can constraint the search space by providing templates for function symbols, and constraints on the size of the universe and range of functions. |
| Bruno Dutertre, SRI International |
Challenging Problems for Yices Yices is an SMT solver developed at SRI International. We describe recent developments in Yices, then we discuss a few applications that present special challenges for Yices. One application is related to modeling and analysis of biological systems. The other is a scheduling problem for timed-triggered systems. Both classes of applications involve solving large combinations of linear arithmetic constraints. They show the scalability limits of current SMT solvers on constraint satisfaction problems and the significant gap that exist between SMT solvers and other technology such as MILP in these domains. |
| Ulrich Furbach, Universität Koblenz-Landau |
Deduction Based Question Answering This talk introduces the natural language question answering system Loganswer (www.loganswer.de). There will be an emphasis on the embedding of the 1st order KRHyper system and its cooperation with machine learning parts of the system. We will discuss problems which stem from the huge amount of data necessary to query Wikipedia and from the combination with webservices. Applications of Loganswer in the context of question answering forums will also be mentioned. |
| Martin Gebser, Universität Potsdam |
Answer Set Programming, the Solving Paradigm for Knowledge Representation and Reasoning Abstract. Answer Set Programming (ASP; [1,2,3,4]) is a declarative
problem solving approach, combining a rich yet simple modeling language
with high-performance solving capacities. ASP is particularly
suited for modeling problems in the area of Knowledge Representation
and Reasoning involving incomplete, inconsistent, and changing information.
From a formal perspective, ASP allows for solving all search
problems in NP (and NPNP) in a uniform way (being more compact
than SAT). Applications of ASP include automatic synthesis of multiprocessor
systems, decision support systems for NASA shuttle controllers,
reasoning tools in systems biology, and many more. The versatility of
ASP is also reected by the ASP solver clasp [5,6,7], developed at the
University of Potsdam, and winning rst places at ASP'09, PB'09, and
SAT'09. |
| Jürgen Giesl, RWTH Aachen |
Modular Termination Analysis for Java Bytecode by Term Rewriting We present an automated approach to prove termination of Java Bytecode (JBC) programs by automatically transforming them to term rewrite systems (TRSs). In this way, the numerous techniques and tools developed for TRS termination can be used for imperative object-oriented languages like Java, which can be compiled into JBC. For the scalability of the approach, we show how it can be modularized such that methods can be analyzed separately and such that termination of the resulting TRSs can be proved in a modular war. |
| Alberto Griggio, Fondazione Bruno Kessler |
Efficient Interpolant Generation in Satisfiability Modulo Linear Integer Arithmetic
The problem of computing Craig interpolants in SAT and SMT has recently
received a lot of interest, mainly for its applications in formal
verification.
Efficient algorithms for interpolant generation have been presented for
some theories of interest ---including that of equality and
uninterpreted functions, linear arithmetic over the rationals, and their
combination--- and they are successfully used within model checking
tools. |
| Reiner Hähnle, Chalmers University of Technology |
Implementing a partial evaluator via a software verification tool We present how to realize a partial evaluator for Java source code programs using a symbolic execution driven verification system. Partial evaluation is a program specialization technique that allows to optimize programs for which partial input is known. Our approach works in two phases: The first phase analysis the Java source code wrt possible preconditions/invariants. During the analysis phase symbolic execution steps are interleaved with calls to a native partial evaluator and first-order reasoning is used to detect infeasible branches. In the second phase, we synthesize the specialized program from the resulting symbolic execution tree. While we focus in this paper on Java source code as target language, it is noteworthy that decoupling the analysis and synthesis phase allows us to also exchange the target language by, for instance, Java Bytecode. A prototypical system as an extension to the KeY verification system is currently under development. |
| Krystof Hoder, University of Manchester |
Sine Qua Non for Large Theory Reasoning Reasoning with very large theories expressed in first-order logic can
strongly benefit from a good selection method for relevant axioms.
This is confirmed by the fact that the largest available first-order
knowledge base (the Open CYC) contains over 3 million axioms, while
answering queries to it usually requires not more than a few dozen
axioms. |
| Ian Horrocks, University of Oxford |
Searching for the Holy Grail In this talk I will review my personal odyssey from Grail to the Semantic Web and back again: a fifteen-year (and counting) mission to explore strange new worlds; to seek out new logics and new applications; to boldly go where no description logician has gone before. I will try to identify important lessons that I have learned along the way about the theory and practice of logic based knowledge representation (and I will try to avoid further mixing of metaphors). In particular, I will review the evolution of ontology systems to date, show how DL theory developed into a mainstream technology, and present some examples of successful (and not to successful) applications. I will then go on to examine the challenges arising from the deployment of reasoning systems in large scale applications, and discuss recent research aimed at addressing these challenges. |
| Paul B. Jackson, University of Edinburgh |
Improved techniques for proving non-linear real arithmetic problems I'll survey the work of my PhD student Grant Passmore on his RAHD prover. RAHD heuristically combines a variety of different reasoning techniques, aiming to exploit the strengths of each. For example it makes use of Groebner Basis computations and CAD (cylindrical algebraic decomposition) procedures. I'll touch on recent developments which include a new variation on CAD that brings in the use of extra proof procedures to `short-circuit' expensive computations during the lifting phase of CAD. I'll also make a few remarks on a just-started project to integrate RAHD with Larry Paulson's MetiTarski system for reasoning with transcendental functions and to explore applications to hybrid systems verification. |
|
Dejan Jovanovic, New York University
|
Sharing is Caring: Combination of Theories One of the main shortcomings of the traditional methods for combining theories is the complexity of guessing the arrangement of the variables shared by the individual theories. This paper presents a reformulation of the Nelson-Oppen method that takes into account explicit equality propagation and can ignore pairs of shared variables that the theories do not care about. We show the correctness of the new approach and present care functions for the theories of uninterpreted functions and the theory of arrays. The effectiveness of the new method is illustrated by experimental results demonstrating a dramatic performance improvement on benchmarks combining arrays and bit-vectors. Cutting to the Chase: Solving Linear Integer Arithmetic I'll describe a new algorithm for solving linear integer programming problems. The algorithm performs a DPLL style search for a feasible assignment, while using a novel cut procedure to guide the search away from the conflicting states. |
| Tommi Junttila, Aalto University |
SAT Solving in Grids: Randomization, Partitioning, and Clause Learning (Joint work with Antti Hyvarinen and Ilkka Niemela) |
| Deepak Kapur, University of New Mexico |
A Quantifier-Elimination Heuristic for Octagonal Constraints Octagonal constraints expressing weakly relational numerical
properties of the form ($l \le \pm x \pm y \leq
h$) have been found useful and effective in static analysis of
numerical programs. Their analysis serves as a key component of
the tool ASTREE based on abstract interpretation framework
proposed by Patrick Cousot and his group, which has been
successfully used to analyze commercial software consisting of
hundreds of thousand of lines of code. This talk will discuss a
heuristic based on the quantifier-elimination (QE) approach presented by
Kapur (2005) that can be used to automatically derive loop invariants
expressed as a conjunction of octagonal constraints in $O(n^2)$,
where $n$ is the number of program variables over which these
constraints are expressed. This is in contrast to the algorithms
developed in Mine's thesis which have the complexity at least
$O(n^3)$. The restricted QE heuristic usually generates invariants stronger than those
obtained by the freely available Interproc tool. |
| Vladimir Klebanov, Karlsruhe Institute of Technology |
You are in a twisty maze of proofs, all alike Scaling up deductive program verification to practical application raises many issues that are not reflected in verification theory. These may be due to the complexity of an individual software product, to product cycles and incremental development, or to a development of a (to-be-verified) product family. We present our research on proof slicing, proof management, and proof reuse aiming to alleviate these issues. |
| Konstantin Korovin, University of Manchester |
Labelled Unit Superposition for Instantiation-based Reasoning Efficient equational reasoning is indispensable in many applications.
Integration of efficient equational reasoning into instantiation-based
calculi is a known challenging problem. In this work we investigate an
extension of the Inst-Gen method with superposition-based reasoning,
called Inst-Gen-Eq. One of the distinctive features of the Inst-Gen-Eq
method is a modular combination of ground reasoning based on any
off-the-shelf SMT solver with superposition-based first-order reasoning.
A major challenge in this approach is efficient extraction
of relevant substitutions from superposition proofs, which are used
in the instance generation process.
The problem is non-trivial because we need to explore
potentially all non-redundant superposition proofs,
extract relevant substitutions and efficiently propagate redundancy
elimination from instantiation into superposition derivations.
We address this challenge by introducing a labelled unit superposition
calculus. Labels are used to collect relevant substitutions during
superposition derivations and facilitate efficient instance generation.
We introduce and investigate different label structures based on sets,
AND/OR trees and OBDDs and highlight how the label structure can be
exploited for redundancy elimination. |
| Laura Kovacs, Vienna University of Technology |
Experiments with Invariant Generation Using a Saturation Theorem Prover We evaluate an invariant generation technique proposed recently by us.
The technique is using the first-order theorem
prover Vampire for both generating invariants and minimising the set of
generated invariants. The main ingredient of our approach to invariant generation
is saturation oriented to symbol elimination in the combination of first order logic
and various theories. We discuss implementation details of invariant generation
in Vampire and present experimental results obtained on academic and industrial
benchmarks. The results demonstrate the power of the symbol elimination
method in generating quantified invariants. |
| Florian Lonsing, Johannes Kepler University Linz |
Preprocessing QBF: Failed Literals and Quantified Blocked Clause Elimination Preprocessing the input of a satisfiability solver is a powerful technique to boost solver performance. In this talk we focus on preprocessing quantified boolean formulae (QBF) in prenex CNF. First, we consider failed literal detection (FL). Whereas FL is a common approach in propositional logic (SAT) it cannot easily be applied to QBF. We present two approaches for FL in QBF based on abstraction and Q-resolution. Finally, we generalize blocked clause elimination (BCE) from SAT to QBF, thus obtaining quantified BCE (QBCE). BCE allows to simulate many structural preprocessing techniques in SAT. A similar property holds for QBCE. Experimental evaluation demonstrates that FL and QBCE are able to improve the performance of both search- and elimination-based QBF solvers. |
| Stephan Merz, INRIA Nancy |
The TLA+ Proof System TLA+ is a formal language designed by Leslie Lamport for the specification of concurrent and distributed systems. It is based on mathematical set theory and TLA (the Temporal Logic of Actions), a variant of linear-time temporal logic. Tool support for TLA+ has existed for several years in the form of an explicit-state model checker for the verification of finite instances of specifications. |
| Ilkka Niemela, Aalto University |
Integrating Answer Set Programming and Satisfiability Modulo Theories In this talk we consider the problem of integrating answer set programming (ASP) and satisfiability modulo theories (SMT). We discuss a characterization of stable models of logic programs based on Clark's completion and simple difference constraints. The characterization leads to a method of translating a set of ground logic program rules to a linear size theory in difference logic, i.e. propositional logic extended with difference constraints between two integer variables, such that stable models of the rule set correspond to satisfying assignments of the resulting theory in difference logic. Many of the state-of-the-art SMT solvers support directly difference logic. This opens up interesting possibilities. On one hand, any solver supporting difference logic can be used immediately without modifications as an ASP solver for computing stable models of a logic program by translating the program to a theory in difference logic. On the other hand, SMT solvers typically support also other extensions of propositional logic such as linear real and integer arithmetic, fixed-size bit vectors, arrays, and uninterpreted functions. This suggests interesting opportunities to extend ASP languages with such constraints and to provide effective solver support for the extensions. Using the translation an extended language including logic program rules and, for example, linear real arithmetic can be translated to an extension of propositional logic supported by current SMT solvers. We discuss the effectiveness of state-of-the-art SMT solvers as ASP solvers and the possibilities of developing extended ASP languages based on SMT solver technology. |
| Tobias Nipkow, TU München |
Verified efficient enumeration of graphs modulo isomorphism In the proof of the Kepler conjecture, hundreds of thousands of graphs need to be enumerated and the result needs to be compared modulo isomorphism with a given set of graphs. I will discuss the verification of the algorithms involved, with an emphasis on efficient data structures and algorithms, and their modular composition. |
| Albert Oliveras, Technical University of Catalonia |
Cumulative Scheduling and Pseudo-Boolean Constraints Cumulative Scheduling is the problem of, given a set of tasks that
consume some resources, some precedence constraints between these
tasks and the number of available units for each resource, find a
feasible schedule that minimizes the makespan (i.e. the completion
time of the last task). In the first part of the talk we will show
how a reduction to Pseudo-Boolean constraints is superior to other
solving approaches. |
| Ruzica Piskac, EPFL Lausanne |
Decision Procedures for Automating Termination Proofs Automated termination provers often use the following schema to prove that a program terminates: construct a relational abstraction of the program's transition relation and then show that the relational abstraction is well-founded. The focus of current tools has been on developing sophisticated techniques for constructing the abstractions while relying on known decidable logics (such as linear arithmetic) to express them. We believe we can significantly increase the class of programs that are amenable to automated termination proofs by identifying more expressive decidable logics for reasoning about well-founded relations. In this talk I will present a new decision procedure for reasoning about multiset orderings, which are among the most powerful orderings used to prove termination. I will show how, using our decision procedure, one can automatically prove termination of natural abstractions of programs. |
| Andre Platzer, Carnegie Mellon University |
Quantified Differential Dynamic Logic for Distributed Hybrid Systems We address a fundamental mismatch between the combinations of
dynamics that occur in cyber-physical systems and the limited
kinds of dynamics supported in analysis. Modern applications
combine communication, computation, and control. They may even
form dynamic distributed networks, where neither structure nor
dimension stay the same while the system follows hybrid
dynamics, i.e., mixed discrete and continuous dynamics. |
| Piotr Rudnicki, University of Alberta |
On the Integrity of a Repository of Formal Mathematics The Mizar proof-checking system is used to build the Mizar
Mathematical Library (MML). The Mizar project is a long term effort
aiming at building a comprehensive library of mathematical knowledge.
The language in which mathematics is recorded, the checking software
and the organization of MML evolve. This evolution is driven by the
growing library and continuous revisions of past contributions. |
| Philipp Ruemmer, Uppsala University |
Beyond Quantifier-Free Interpolation in Extensions of Presburger Arithmetic Craig interpolation has emerged as an effective means of generating candidate program invariants. We present interpolation procedures for the theories of Presburger arithmetic combined with (i) uninterpreted predicates (QPA+UP), (ii) uninterpreted functions (QPA+UF) and (iii) extensional arrays (QPA+AR). We prove that none of these combinations can be effectively interpolated without the use of quantifiers, even if the input formulae are quantifier-free. We go on to identify fragments of QPA+UP and QPA+UF with restricted forms of guarded quantification that are closed under interpolation. Formulae in these fragments can easily be mapped to quantifier-free expressions with integer division. For QPA+AR, we formulate a sound interpolation procedure that potentially produces interpolants with unrestricted quantifiers. |
| Ina Schaefer, Braunschweig University of Technology |
Compositional Verification of Software Product Families Software product line engineering aims at developing a set of systems by managed reuse. A product line can be described by a hierarchical variability model specifying the commonalities and variabilities between its individual products. The number of products generated by a hierarchical model is exponential in its size, which poses a serious challenge to software product line and verification. For an analysis technique to scale, their effort has to be linear in the size of the model rather than in the number of products it generates. This is only achievable by compositional verification techniques. |
| Stephan Schulz, TU München |
First-Order Deduction for Large Knowledge Bases The largest TPTP problems now have millions of axioms and take up half
a gigabyte of text even before clausification. The size of problem
specifications has grown much faster than even the capabilities of
hardware. In particularly, it is no longer feasible to parse and
pre-process the complete axiomatization for each individual proof
problem. However, in this setting, proofs are often simple, and user
applications require the execution of multiple queries over a constant
or near-constant knowledge base. |
| Sanjit A. Seshia, University of California, Berkeley |
Voting Machines and Automotive Software: Explorations with SMT at Scale I will describe some recent projects involving SMT solving in the design and analysis of hardware, software and embedded systems. One project is on the design of a verified electronic voting machine, including both internal logic and the user interface. A second project concerns the analysis of quantitative properties of embedded systems, such as timing. In each case, I will describe the application and relate our experience formulating SMT problems as well as developing and using SMT solvers. |
| Natasha Sharygina, University of Lugano |
An efficient and flexible approach to resolution proof reduction A propositional proof of unsatisfiability is a certificate of the unsatisfiability of a Boolean formula. Resolution proofs, as generated by modern SAT solvers, find application in many verification techniques where the size of the proofs considerably affects efficiency. This talk presents a new approach to proof reduction, situated among the purely post-processing methods. The main idea is to reduce the proof size by eliminating redundancies of occurrences of pivots along the proof paths. This is achieved by matching and rewriting local contexts into simpler ones. In our approach, rewriting can be easily customised in the way local contexts are matched, in the amount of transformations to be performed, or in the different application of the rewriting rules. We provide experimental evaluation of our technique on a set of SMT and SAT benchmarks, which shows considerable reduction in the proofs size. |
| Mark Stickel |
|
| Geoff Sutcliffe, University of Miami |
SPASS-XDB - Automated Reasoning with World Knowledge (Joint work with Martin Suda, David Stanovsky, and Gerard de Melo) |
| Philippe Suter, EPFL Lausanne |
Satisfiability Modulo Computable Functions We present an algorithm and the resulting system for reasoning about specifications over algebraic data types, integers and recursive functions. Our algorithm is capable of both 1) finding proofs and 2) generating concrete counterexamples. It interleaves these two complementary search activities using a fair search procedure. Automation comes in part from using the state-of-the-art SMT solver Z3. We prove that our algorithm is terminating for a number of interesting classes of function specifications. (Because it doesn't need to recognize the input as belonging to any particular decidable fragment, it also succeeds for examples outside these fragments.) We have implemented our approach as a system to verify programs written in a purely functional subset of Scala. Using our system, we have verified a number of examples, such as syntax tree manipulations and functional data structure implementations. For incorrect properties, our system typically finds counterexample test cases quickly. |
| Josef Urban, Radboud University Nijmegen |
Large Formal Libraries: Birthplace of Strong AI? Induction (suggesting and learning conjectures, principles, and explanations from data) and deduction (drawing conclusions from principles) are two frequent reasoning methods used by humans. Recently, in the field of formal mathematics, large knowledge bases have been created, containing deep abstract ideas accumulated over centuries in computer-understandable form. This allows AI researchers to experiment with various novel combinations of inductive and deductive reasoning. At the same time, the search space of purely deductive general reasoning tools becomes very large when working over large mathematical theories, and needs to be pruned by suitable heuristic guidance. A promising way how to automatically produce such guidance for large number of problems is again induction, and particularly machine learning from previous solutions. In this talk the field will be shortly introduced. The MaLARea system combining in a closed AI loop automated reasoning tools with machine learning from solved problems will be introduced, and evaluated on a large-theory benchmark. The various existing and possible ways of how to do machine learning over large bodies of computer-understandable mathematics will be discussed. |
| Andrei Voronkov, University of Manchester |
Propositional Variables and Splitting in a First-Order Theorem Prover It is often the case that first-order problems contain propositional
variables and that proof-search generates many clauses that can be split
into components with disjoint sets of variables. This is especially true
for problems coming from applications, where many ground (that is,
variable-free) literals occur in the problems and even more are generated. |
| Christoph Weidenbach, MPI for Informatics |
The Model-Based Car Lifecycle - A Challenge to Automated Reasoning Today car manufactures use a huge variety of IT systems to cover the lifecycle of a car. The range starts from drawing support at the design phase, over CAX, simulation, and software development systems for product development, all kinds of planning and layout systems for product engineering, systems for finance, marketing, sales and finally after sales. Current state of the art is that all those systems are at most loosely coupled. As a result, bugs or deficiencies that require the composition of information among the different systems are often not discovered. Or they show up too late at the customer. What does it mean to automated reasoning if we build a global car model incorporating relevant information from all used systems? |
| Patrick Wischnewski, MPI for Informatics |
YAGO++ Query Answering YAGO is an automatically generated ontology out of Wikipedia and WordNet. A core comprises 10 million facts and formulas. Previously, we showed how to check satisfiability of overall YAGO in less than one hour and how to answer non-trivial existentially quantified queries. YAGO++ properly extends YAGO by further classes of Horn axioms and in particular, negative facts. Satisfiability for YAGO++ can still be checked in one hour due to improved data structures and specific superposition calculi. Furthermore, our approach now supports query answering for arbitrary quantifier alternations on the basis of the minimal model of YAGO++. Queries are typically processed in less than one second. |
| Harald Zankl, University of Innsbruck |
Labelings for Decreasing Diagrams This talk is concerned with automating the decreasing diagrams technique of van Oostrom for establishing confluence of term rewrite systems. We build on recent work (van Oostrom 2008), (Aoto 2010), and (Hirokawa and Middeldorp 2010) and study abstract criteria that allow to lexicographically combine labelings to show local diagrams decreasing. This approach has two immediate benefits. First, it allows to use labelings for linear rewrite systems also for left-linear ones, provided some mild conditions are satisfied. Second, it admits an incremental method for proving confluence which subsumes recent developments in automating decreasing diagrams. The proposed techniques have been implemented into the confluence prover CSI and experimental results demonstrate how, e.g., the rule labeling benefits from our contributions. |
Accommodation
There will be rooms available at Ringberg Castle. We also reserved rooms at Gästehaus Leykauf, which is located near the castle. We will give you further details about your accomodation after registration.
The full board rate is 100 Euros per day. We will try to arrange a contribution to the costs for students. Please pay for the accomodation at departure.
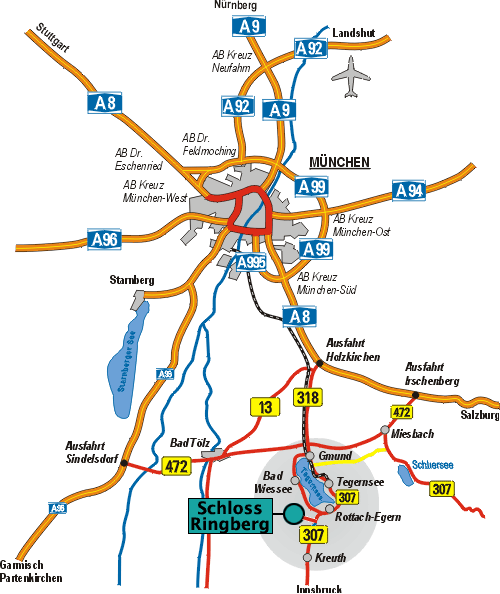
Arrival / Directions
Arriving by Plane at the Munich Airport
On arrival, proceed to the S-Bahn (city railway) station below the central area of the terminal. To find it, follow the signs. (On this map it is located at the bottom). Between 6:55 and 22:15 trains for downtown Munich leave at 20 minute intervals (first train at 3:55, the last at 0:55). There are ticket vending machines just before the escalators that take you down to the S-Bahn platform. Press the number 8 button and feed the machine the amount it displays (10,20 Euro as of September 2004). The machines will accept coins and 10 and 20 Euro bills. See schedule plan for more information. Next, you have to stamp your ticket at one of the blue endorsing machines (marked with an "E" on a yellow square) you find close to the escalators. You can take any train starting there; after about 40 minutes get off at the "Hauptbahnhof" (central station). Remember to leave the train through the doors on the right side. (No joke. The left doors are only for entering the train at some stations. You'll find no "Exit" signs on the left-hand platform.) You will have to take two escalators up to the station's main level. Follow the signs (Deutsche Bahn). There are ticket offices on the intermediate level (The sign says "Fahrkarten"). Get a ticket for "Tegernsee" (10,20 Euro, 2nd class, single fare as of September 2004). You find the departure times on the schedule. To make your quest for Ringberg a bit harder, the trains for Tegernsee do not leave from the platforms in the station's main building, but from one of the well hidden platforms (numbers 27 to 36) at the north-west wing: When you have finally located located the train (see the signs) you have still to find out the right car to sit in: only one of them will go to Tegernsee. Have a look a the labels on the cars or ask the friendly conductor. When you finally made it to Tegernsee, take a cab to get you the last miles to Ringberg Castle.
Arriving by Car
Address for car navigation:
Schloss Ringberg
Schlossstrasse 20
83708 Kreuth
Organization and Contact
General Organization
Local Organization
For comments or questions send an email to Jennifer Müller (jmueller (at) mpi-inf.mpg.de).
Important Dates
- Registration Deadline: 2010/09/30
- Deadline for Title and Abstract: 2011/02/04
- Seminar: 2011/03/07 - 2011/03/11
